Les nombres premiers constants

Depuis des millénaires, les nombres premiers fascinent les mathématiciens. On les connaît comme les “briques” fondamentales des nombres entiers, indivisibles, essentiels en cryptographie, en théorie des nombres et dans l’histoire des mathématiques.
Mais une nouvelle classe vient aujourd’hui enrichir leur univers : les nombres premiers constants (base 8 et 10). Référencé sur le site OEIS

🔢 Qu’est-ce qu’un nombre premier constant ?

Prenez un nombre premier, par exemple 83. Additionnez ses chiffres : 8 + 3 = 11.
Additionnez encore les chiffres du résultat : 1 + 1 = 2.
À chaque étape, on continue à additionner les chiffres du nombre obtenu, jusqu’à arriver à un chiffre unique.

Ce processus est appelé réduction numérique ou somme digitale récursive.

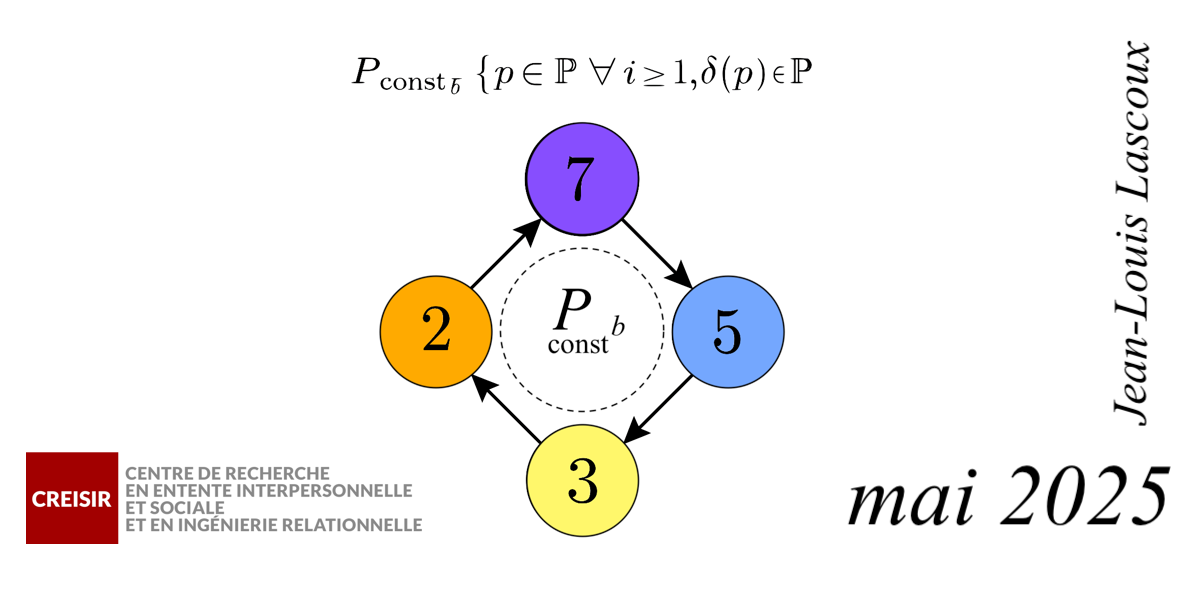
👉 Un nombre premier constant est un nombre premier pour lequel toutes les étapes de cette réduction donnent encore des nombres premiers, jusqu’au chiffre final.

📍 Quelques exemples :

2, 3, 5, 7, 131, 311, 887

• 131 → 1+ 3+1 = 5  ✔ (premier constant)

• 311 → + 3 + 1 + 1 = 5 ✔ (premier constant)

• 887 → 8 + 8 + 7 = 23 (premier) → 2 + 3 = 5 (premier constant)

🧠 Pourquoi est-ce intéressant ?

Les nombres premiers constants forment une famille nouvelle, définie par une propriété numérique interne.
Ils ne sont pas seulement premiers : ils sont stables lorsqu’on les “réduit” par leurs chiffres.
Cette stabilité numérique en fait des objets remarquables, à la frontière entre la mathématique pure, la symbolique et l’informatique.

🧪 Ma découverte

• Il existe une infinité de nombres premiers constants, mais c’est encore plus intéressant d’observer un suite sur plusieurs bases. Ici, je n’ai pris que deux bases, mais j’ai déjà fait plusieurs observations sur un ensemble de bases. Et quoi ?

  • Leur comportement est régulier, prévisible dans certains cas, et profondément lié à des propriétés cachées des chiffres.

  • Ils pourraient jouer un rôle dans le codage numérique, la cryptographie, voire la modélisation de structures stables en intelligence artificielle.

📚 En résumé

Les nombres premiers constants sont comme des primes résilients :
même quand on les décompose par leurs chiffres,
ils continuent à rester premiers, à chaque étape.

Ils incarnent une nouvelle façon de regarder les nombres premiers, non plus seulement comme objets isolés, mais comme trajectoires stables dans l’univers des chiffres.

sur l’encyclopédie des nombres entiers oeis.org