Ajustativité dynamique et barycentrisme fractal : fondements formels de la Théorie de l’Ajustativité Générale (TAG)
Si vous connaissez les problèmes posés par Stanislaw Ulam, vous êtes bon pour être de mes lecteurs sur ce coup-là.
Cet article pose les fondations formelles de la Théorie de l’Ajustativité Générale (#TAG), une approche transdisciplinaire qui définit tout système dynamique comme une structure en ajustement permanent entre ses composantes, son contexte, et l’intensité de ses interactions. J’ai conçu la formule opérative ∆A = K ⋅ Φ ⋅ I, et déploie une modélisation géométrique fondée sur le DT-FRACTAL®, une structure fractale barycentrique à base de tétraèdres imbriqués centrés sur leur Fractocentre®. Ce cadre ouvre une voie d’unification entre la physique, la cognition, la biologie et l’ingénierie des systèmes complexes.
1. Introduction : limites des paradigmes prédictifs
Les modèles dominants en physique et en neurosciences reposent sur la prédictivité : anticiper le futur à partir de données passées. Or, dans les systèmes complexes, ouverts et sensibles à leur environnement, cette approche montre ses limites. La TAG propose un paradigme alternatif fondé sur l’ajustement dynamique présentiel.
2. La formule de l’ajustativité : ∆A = K ⋅ Φ ⋅ I
Cette formule constitue l’axiome opératif de la TAG :
-
∆A : variation du niveau d’ajustativité d’un système
-
K : structure contextuelle (topologie, contraintes, cadre)
-
Φ : phase ou synchronisation dynamique entre les éléments
-
I : intensité des interactions effectives
Cette équation permet de modéliser le comportement d’un système vivant, physique ou cognitif sans recourir à une causalité linéaire.
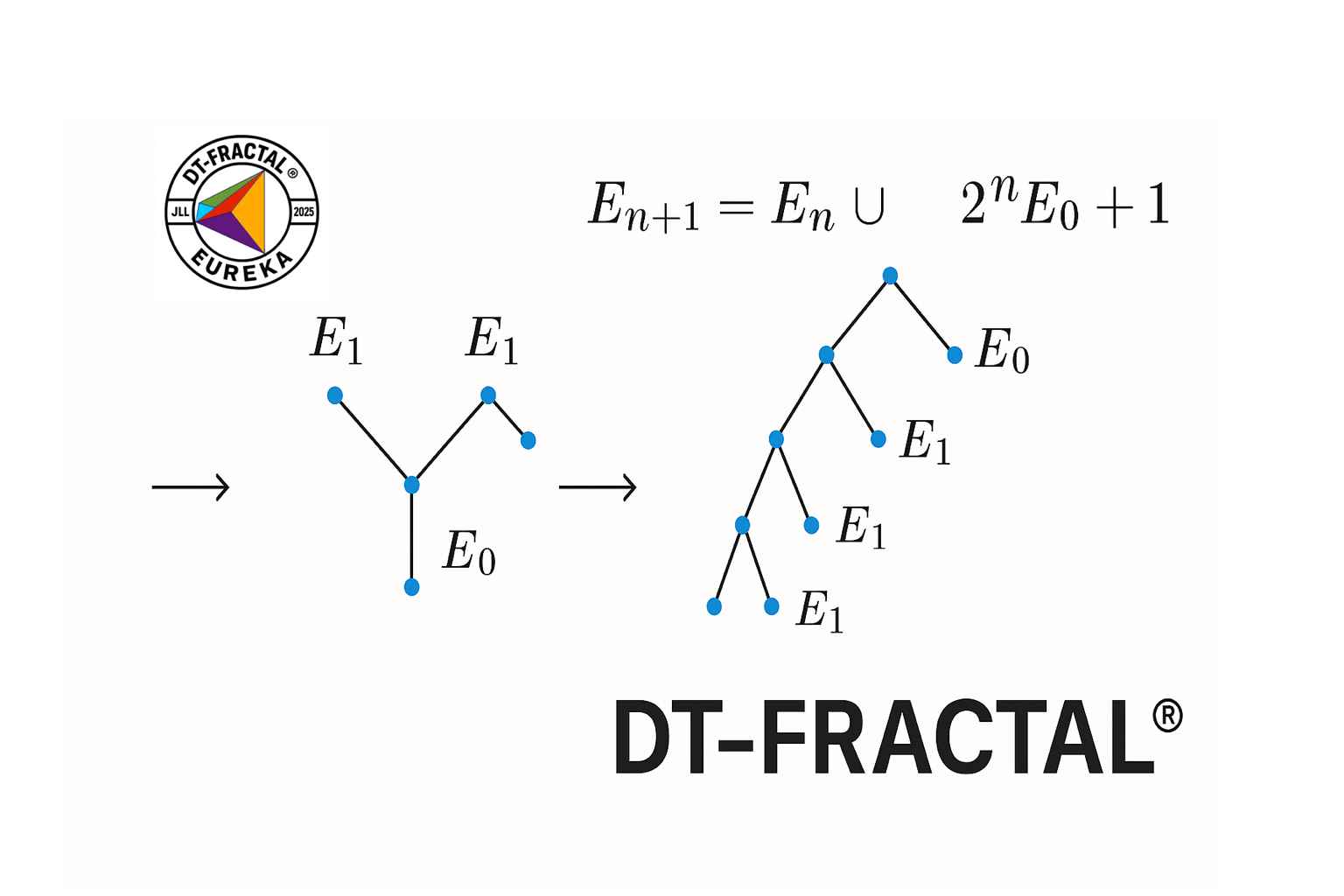
3. Le modèle géométrique DT-FRACTAL®
J’introduisons ici la structure DT-FRACTAL® : un réseau fractal de tétraèdres organisés autour d’un barycentre dynamique appelé Fractocentre®. Chaque subdivision conserve une symétrie d’orientation et une isotropie relative par rapport au centre d’ajustement local.
4. Barycentrisme et cohérence : équation de stabilité
Une autre formule fondamentale de la TAG est donnée et représente le Fractocentre®, barycentre dynamique pondéré par le niveau d’ajustement local de chaque composant. Cette formule permet d’évaluer la stabilité d’un système quel que soit son degré de complexité.
5. Interprétations et domaines d’application
Ce formalisme permet d’aborder de façon unifiée :
-
La régulation dynamique des systèmes physiques non linéaires
-
Les processus d’ajustement en neurosciences (plasticité, attention, apprentissage)
-
Les équilibres biologiques adaptatifs
-
Les systèmes sociaux et organisationnels en tension
6. Conclusion et perspectives
La TAG et son formalisme fractal offrent un cadre robuste pour réinterpréter des phénomènes dispersés par discipline en une dynamique commune d’ajustement.
Avec ce modèle, j’ai apporté une solution à la question de la flottabilité isotrope (problème d’Ulam). Il en a résulté une déclinaison de simulations multiscalaires pour la validation du DT-FRACTAL® dans divers systèmes complexes, comme l’identification d’erreurs multiples. Et maintenant, je me retrouve dans la baignoire d’Archimède…
7. Ca vous branche : connectez-vous ! Je suis à votre écoute
Mots-clés : #ajustativité, #TAG, #systèmes complexes, #dynamique, #fractal, #cognition, #modélisation, #physique, #neurosciences, médiation, #management #sondage
Ps : toutes ces recherches et leurs applications font l’objet de protections internationales