Une suite géométrique issue de la subdivision tétraédrique d’un octaèdre régulier
Introduction
Parmi les nombreuses façons de générer des suites d’entiers à partir de constructions géométriques, certaines se distinguent par leur simplicité formelle et leur richesse structurante. La nouvelle suite : Number of tetrahedra formed by iterative 4-ary subdivision of a regular stellar bitetrahedron (Stella Octangula configuration), starting from 8 initial tetrahedra est de celles-là.
Elle émerge d’un processus élémentaire et pourtant puissamment combinatoire :
subdiviser récursivement un ensemble de tétraèdres dans l’espace à partir d’un octaèdre régulier.
Décomposition initiale : de l’octaèdre au Stella Octangula
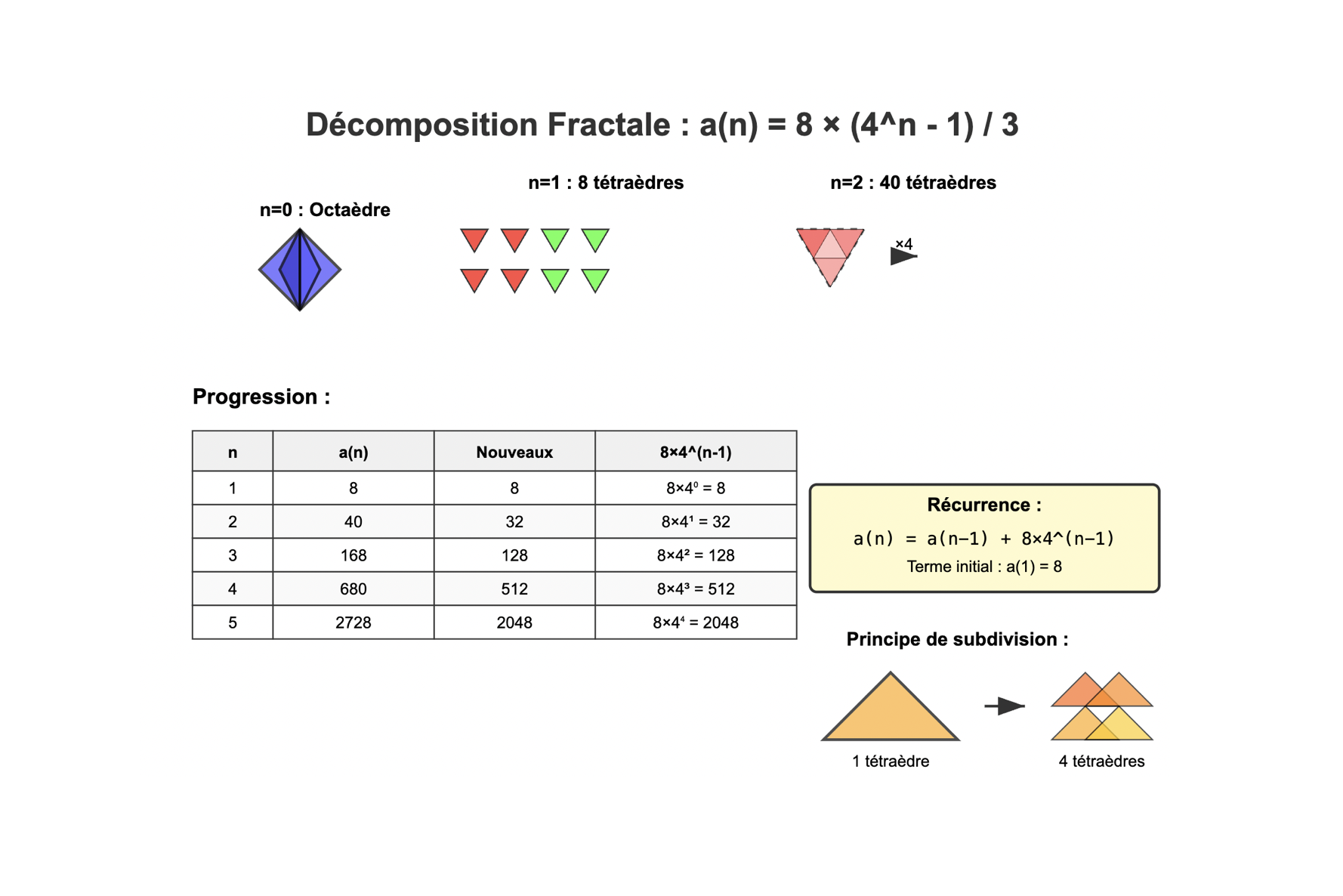
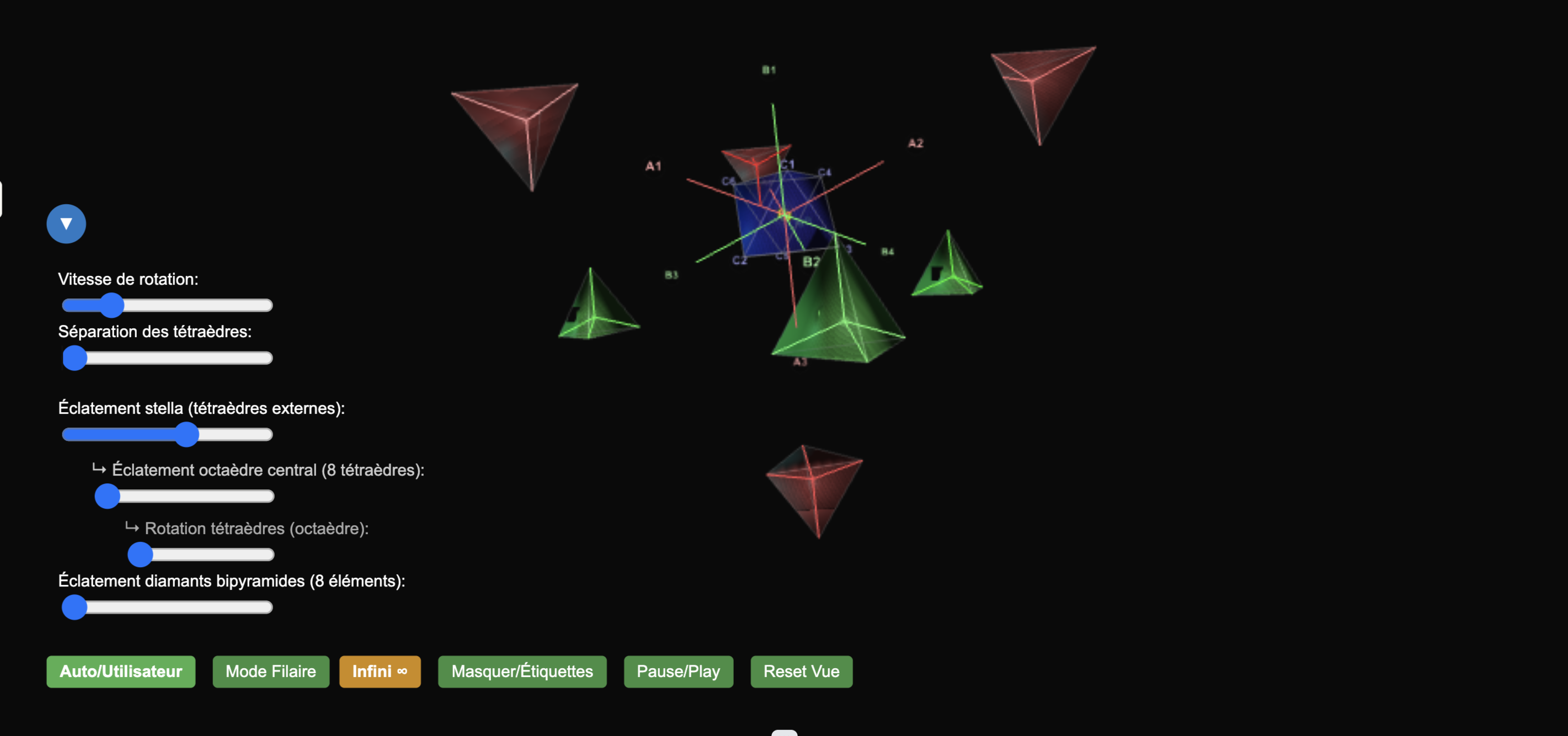
Considérons un octaèdre régulier, polyèdre de Platon à 8 faces triangulaires. En disposant deux tétraèdres réguliers emboîtés dans un cube (symétriquement opposés), on forme la Stella Octangula : une étoile géométrique dont l’intersection forme un octaèdre central.
Cet octaèdre peut être décomposé en 8 tétraèdres réguliers identiques, chacun occupant une portion symétrique de l’espace. Cette configuration initiale fournit le point de départ :
a(1)=8a(1) = 8
Subdivision récursive 4-aire
À chaque étape suivante, on applique la règle suivante :
Chaque tétraèdre est subdivisé en 4 tétraèdres plus petits, congruents au sein du volume initial.
Ce processus est récursif, homogène et volume-remplissant :
-
Tous les tétraèdres générés à un niveau
nsont subdivisés à l’identique au niveaun+1, -
Aucun chevauchement, aucune lacune : le volume global est conservé,
-
La symétrie octaédrique est préservée à chaque étape.
La nouvelle suite
Le nombre total de tétraèdres après n étapes est donné par la formule fermée :
a(n)=8(4n−1)3,n≥1a(n) = \frac{8(4^n – 1)}{3}, \quad n \geq 1
Les premiers termes sont :
La récurrence vérifiée par cette suite est :
a(n)=5a(n−1)−4a(n−2),n≥3a(n) = 5a(n-1) – 4a(n-2), \quad n \geq 3
Et plus directement :
a(n)=a(n−1)+8⋅4n−1a(n) = a(n-1) + 8 \cdot 4^{n-1}
Chaque étape ajoute 8 fois plus de tétraèdres que celle d’avant à l’ordre n-1, ce qui traduit une croissance exponentielle strictement contrôlée.
Interprétation fractale
Ce processus produit une structure fractale tridimensionnelle, analogue en 3D à ce que représente le tapis de Sierpiński en 2D.
La fractale :
-
Est auto-similaire à chaque étape,
-
Suit un schéma de subdivision régulier et affine,
-
Conserve l’intégrité du volume global à toute profondeur.
Il s’agit donc d’un fractal de remplissage, et non d’un fractal lacunaire.
Propriétés géométriques
| Propriété | Valeur |
|---|---|
| Structure initiale | 8 tétraèdres réguliers dans un octaèdre |
| Type de subdivision | 4-aire (chaque tétraèdre → 4 tétraèdres) |
| Facteur de croissance local | ×4 |
| Facteur de croissance global | ×5 – 4 (récurrence linéaire homogène d’ordre 2) |
| Dimension fractale | D = log(4)/log(2) = 2 |
| Applications potentielles | Maillages, modélisation fractale, géométrie 3D |
Comparaisons
Cette suite est numériquement liée à la suite classique :
A002450(n)=4n−13A002450(n) = \frac{4^n – 1}{3}
Mais elle s’en distingue :
-
par son origine géométrique canonique (le facteur 8 est imposé par la structure initiale),
-
par son rôle de modélisation spatiale réelle,
-
par ses applications spécifiques en 3D (infographie, simulation physique, structures hiérarchiques).
Potentiels
-
Maillages adaptatifs 3D : chaque subdivision affine le maillage de façon uniforme, sans compromettre la topologie.
-
Fractales tridimensionnelles : le modèle génère une structure pleinement volumique, auto-similaire.
-
Cristallographie théorique : certaines structures atomiques peuvent être modélisées par des emboîtements de tétraèdres.
-
Visualisation pédagogique : outil idéal pour introduire la notion de fractale 3D concrète.