Mathématiques & Géométrie
06Sep

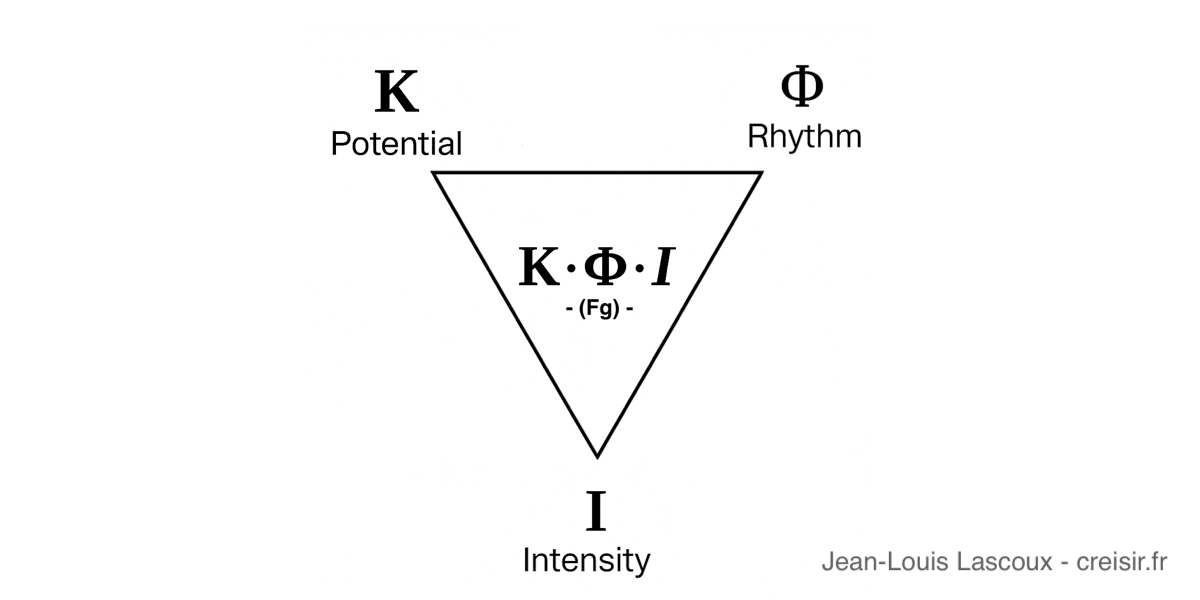
Ces années que nos horloges numériques ne montreront jamais / These Years That Our Digital Clocks Will Never Show

Le hasard des lectures numériques réserve parfois des paradoxes temporels et met en évidence des conceptions culturelles de la relation au temps. Partons d’une expérience de pensée simple…

The randomness of digital readings sometimes reveals temporal paradoxes and highlights cultural conceptions of our relationship with time. Let us start with a simple thought experiment…

Une observation anodine / An Ordinary Observation

Il est 19:57 (format 24 h, usage courant en Europe). En jetant un coup d’œil à mon téléphone, mon esprit fait un saut dans le temps : je lis « 1957 ». A ce moment, je sais que ce n’est pas le réel qui s’affiche, mais une convention qui me projette son récit. Me vient alors une question en apparence triviale — toutes les années peuvent-elles s’afficher sur un cadran au format 24 h ?

Réponse : non. Pas plus que pour tous les autres formats.

It is 19:57 (24-hour format, common usage in Europe). Glancing at my phone, my mind makes a leap through time: I read "1957". At this moment, I know that what is displayed is not reality, but a convention projecting its narrative to me. A seemingly trivial question then comes to mind—can all years be displayed on a 24-hour format clock face?

Answer: no. No more than for any other formats.

De l’analogie à la règle / From Analogy to Rule

Une horloge numérique affiche HH:MM (heures : minutes). Pour qu’une année ABCD (AB = deux premiers chiffres, CD = deux derniers) se lise comme une heure valide, deux conditions strictes s’imposent :

  • Heures : AB ∈ [00, 23]
  • Minutes : CD ∈ [00, 59]

Condition d’affichabilité : une année est « affichable » si et seulement si AB ∈ [00, 23] et CD ∈ [00, 59].

A digital clock displays HH:MM (hours:minutes). For a year ABCD (AB = first two digits, CD = last two) to be read as a valid time, two strict conditions must be met:

  • Hours: AB ∈ [00, 23]
  • Minutes: CD ∈ [00, 59]

Displayability condition: a year is "displayable" if and only if AB ∈ [00, 23] and CD ∈ [00, 59].

Application et exemples

Années valides

  • 1957 → AB = 19 (≤ 23), CD = 57 (≤ 59)
  • 2024 → AB = 20 (≤ 23), CD = 24 (≤ 59)
  • 2359 → AB = 23 (≤ 23), CD = 59 (≤ 59) → dernière année valide
  • 0001 → AB = 00 (≤ 23), CD = 01 (≤ 59)

Années invalides

  • 1960 → CD = 60 (> 59) → impossible (après 19:59 vient 20:00)
  • 1999 → CD = 99 (> 59)
  • 2400 → AB = 24 (> 23) → impossible (après 23:59 vient 00:00)

Note : 2024 est une année valide et 20:24 une heure valide. L’illusion de son « impossibilité » vient d’une confusion avec le passage de siècle ; le critère est purement numérique.

Quantification du phénomène (0000 à 9999)*

  • Minutes invalides : pour chaque AB ∈ [00, 23], 40 valeurs interdites de CD (60–99).
    → 24 × 40 = 960 années invalides.
  • Heures invalides : toute année ≥ 2400 est invalide.
    → de 2400 à 9999 inclus = 7 600 années invalides.

Total invalides = 960 + 7 600 = 8 560 années.
Total valides = 10 000 – 8 560 = 1 440 années.

* Convention purement numérique : intervalle 0000–9999, indépendamment des calendriers historiques.

Visualisation

PériodeStatutConditionExemplesNombre
0000–2399InvalidesCD ≥ 600060–0099, …, 2360–2399960
2400–9999InvalidesAB ≥ 242400, 2401, …, 99997 600
0000–2359ValidesAB ∈ [00,23], CD ∈ [00,59]0000–0059, …, 2300–23591 440
Total———10 000

Le filtre temporel de l’horloge / The Clock's Temporal Filter

Notre manière de compter les heures impose un filtre numérique : seules 1 440 années sur 10 000 (soit 14,4 %) peuvent apparaître comme une heure valide sur un cadran 24 h.

La prochaine fois que vous verrez 20:59, pensez que 2059 fait partie de ce club restreint des années qui coïncident, même brièvement, avec une heure réelle de la journée.

Our way of counting hours imposes a numerical filter: only 1,440 years out of 10,000 (or 14.4%) can appear as a valid time on a 24-hour clock face.

The next time you see 20:59, think that 2059 is part of this restricted club of years that coincide, however briefly, with a real time of day.

Du calcul à l’interprétation

Sur le plan strictement numérique, la règle est claire :

Une année ABCD est affichable si et seulement si AB ∈ [00, 23] et CD ∈ [00, 59].
Cela représente 14,4 % des années (1 440 sur 10 000). La dernière année affichable est 2359.

Ce résultat nous rappelle que le temps que nous lisons n’est pas une donnée brute de la réalité, mais une convention. Changer de format (24 h ↔ 12 h, lecture gauche ↔ droite) change ce qui est « possible » d’afficher. Autrement dit, la manière de chiffrer nos cadrans conditionne la perception que nous avons du temps.

De la convention à la perception / From Convention to Perception

À 19:59, il suffit d’une minute pour passer à 20:00 : ce saut peut se lire comme une image — une sorte de « saut quantique » métaphorique. En un instant, on a basculé de 1959 à 2000, comme si l’horloge compressait 40 ans en un battement numérique.

Le temps est une fable de cadran : notre perception suit la convention, et la convention oriente nos croyances.

  • Avec un découpage en 24 heures, on se sent inscrit dans une continuité linéaire.
  • Avec un découpage en deux cycles de 12 heures, certains auront l’impression de disposer d’un temps plus écourté nécessitant plus d’empressement.

Ainsi, le temps que nous mesurons est d’abord un temps que nous racontons. Les chiffres filtrent nos expériences, et chaque convention d’affichage devient une mise en scène culturelle du temps qui dépend, non pas de la réalité du moment, mais de ceux qui la tissent après coup.

At 19:59, it takes just one minute to reach 20:00: this jump can be read as an image—a sort of metaphorical "quantum leap". In an instant, we have jumped from 1959 to 2000, as if the clock compressed 40 years into a digital beat.

Time is a fable of the clock face: our perception follows convention, and convention guides our beliefs.

  • With a 24-hour division, we feel inscribed in a linear continuity.
  • With a division into two 12-hour cycles, some will have the impression of having more limited time requiring more urgency.

Thus, the time we measure is first and foremost a time we narrate. Numbers filter our experiences, and each display convention becomes a cultural staging of time that depends, not on the reality of the moment, but on those who weave it after the fact.

Par Mathématiques & Géométrie
Lire la suite...
02Août

A Bifractal Integer Sequence from Recursive Subdivision of the Stella Octangula

Croissance bifractale tétraédrique : une suite entière dérivée de la subdivision récursive de la Stella Octangula

Fractale stella octangula : une suite géométrique bifractale à potentiel théorique et industriel

Introduction philosophique

La manière dont nous voyons le monde conditionne profondément la manière dont nous le vivons. Cela peut sembler paradoxal, voire non académique, de commencer une étude mathématique par une réflexion d’ordre philosophique. Tant pis. Je n’ai pas été formé par les voies académiques traditionnelles : je suis autodidacte — en tout, y compris dans ce que j’appelle le tourisme existentiel. Certaines visions du monde projettent partout des arrondis, des courbes lissées, comme si adoucir les contours était la voie naturelle vers l’harmonie. C’est une illusion. Il n’y a rien de plus complexe, ni de plus exigeant, que d’arrondir véritablement les angles. Car ce geste — en apparence simple — exige un ajustement précis entre des éléments dissemblables, une gestion des tensions, et une tendance à négocier les points de rupture. On y retrouve les fondements des modèles de pensée économiques, administratifs, managériaux, avec tout le lexique qui les façonnent. C’est à partir de cette relecture fondatrice entre angle et arrondi, entre structure et adaptation, que je propose ici une approche bifractale : géométrique dans sa forme, mathématique dans son expression, philosophique dans sa visée.
Définie en 1509 par Luca Pacioli dans son traité De Divina Proportione, l’objet dont le nom de Stella Octangula sera donné par Johannes Kepler, est initialement pensée comme un symbole de proportion divine, dans l’esprit néoplatonicien de la Renaissance. Les illustrations de Léonard de Vinci lui confèrent un statut emblématique d’harmonie géométrique incarnée. Elle est redécouverte en 1609 par Johannes Kepler, qui y voit une forme parfaite, résultant de l’interpénétration de deux tétraèdres réguliers inversés. Plus tard, Leonhard Euler (1707–1783) formule la relation topologique fondamentale V−E+F=2, marquant une étape décisive dans la formalisation des structures closes. Ce progrès, en apparence neutre, tend paradoxalement à enfermer la Stella Octangula dans une lecture statique et figée. Ma proposition s’inscrit dans une tout autre logique : réouvrir la figure vers des perspectives dynamiques et systémiques, en la réinscrivant dans le champ des fractales, concept introduit dans les années 1970 par Benoît Mandelbrot. L’application bifractale présentée ici vise à détacher la Stella Octangula de sa clôture topologique traditionnelle, pour en faire le support d’une croissance récursive ajustative, à la fois volumique (8-aire) et planaire (4-aire). C’est cette réinterprétation structurelle qui justifie mon choix de l’appeler désormais Bi-Tétraèdre Stellaire : ·       une appellation qui insiste sur son potentiel combinatoire, ·       sa dynamique de subdivision (organisée autour d’un Fractocentre®, et non d’un barycentre académique), ·       et sa capacité de déploiement hiérarchisé dans des modèles fractals d’ingénierie. Il ne s’agit plus d’un simple objet géométrique : c’est un modèle opératif, à la croisée de la précision mathématique, de la complexité fractale, et d’une visée systémique ajustative.
Dans cette recherche, la Stella Octangula– sur laquelle je reviens en nommant la structure « Bi-Tétraèdre stellaire », devient plus qu’un objet de curiosité géométrique : elle s’impose comme une autre forme de pensée. En effet, formée par l’interpénétration parfaite de deux tétraèdres opposés, elle incarne une tension équilibrée entre dualité et symétrie, entre stabilité et expansion. Ce n’est pas tant la figure elle-même qui importe, que la manière dont elle peut être subdivisée, régénérée, complexifiée — sans jamais perdre son principe d’organisation, avec une tonalité nouvelle associée à la liberté. Ce processus de subdivision, je le nomme ici bifractale, parce qu’il repose sur deux lois de croissance distinctes mais coordonnées. L’une est volumique, l’autre est planaire ; l’une s’appuie sur la démultiplication, l’autre sur la structuration. Ensemble, elles génèrent une dynamique hiérarchique d’une remarquable cohérence. Mais pourquoi s’y intéresser ? Parce qu’en modélisant cette croissance, en l’analysant sous forme d’une suite entière bien définie, nous accédons à plus qu’un simple jeu de nombres. Nous touchons à un modèle opératif d’ajustement. Un modèle qui relie le discret et le continu, le local et le global, l’ordre mathématique et la plasticité du réel. Ce lien entre pensée, structure et ajustement n’est pas nouveau. Il remonte à Pythagore, souvent considéré comme l’inventeur du mot philosophie – philo-sophia, l’amour de la sagesse. D’après Diogène Laërce[1], Pythagore aurait introduit ce terme pour désigner une posture de recherche désintéressée, tournée vers l’harmonie des lois universelles. Mais il ne s’agissait pas d’une sagesse vague ou contemplative : pour Pythagore, cette quête passait nécessairement par les nombres, les figures, les rapports. C’est à travers le langage mathématique et géométrique qu’il percevait l’ordre caché du cosmos, et c’est à travers cette exigence qu’il fondait une discipline intérieure. Revenir à la Stella Octangula, Bi-Tétraèdre Stellaire, avec une attention moderne, combinatoire, algorithmique, n’est donc pas un détournement du sens philosophique initial. C’est, au contraire, une fidélité profonde à l’idée pythagoricienne d’une sagesse en actes, qui cherche à comprendre le monde en le structurant — non pour le simplifier, mais pour mieux épouser sa complexité. C’est ainsi que j’ai développé un ensemble théorico-pratique qui touche à la fois au fonctionnement personnel (la théorie du cerveau corrélatif et de l’harmonisation ajustative (TCC-HA), la théorie de l’ajustativité temporelle (T.AJT), les deux réunies en Théorie de l’Ajustativité Générale (#TAG). C’est ambitieux, j’en conviens. Pour autant, cette approche est cohérente et se retrouve opérationnelle, en premier lieu, dans les contextes relationnels humains, puisque c’est là que j’ai développé la première application de mon modèle géométrique, la médiation professionnelle, la profession de médiateur fondée sur la qualité relationnelle et l’Ingénierie Systémique Relationnelle®. À partir de cette articulation entre structure géométrique, dynamique d’ajustement et modélisation relationnelle, nous pouvons formuler une expression mathématique rigoureuse de la croissance bifractale associée à la Stella Octangula. Cette modélisation conduit naturellement à une suite entière a(n), dont chaque terme représente le nombre total de tétraèdres présents à l’itération n d’un processus récursif de subdivision. Ce processus repose sur deux lois complémentaires :
  • une subdivision volumique 8-aire, appliquée aux tétraèdres externes de la structure ;
  • une subdivision planaire 4-aire, centrée sur le cœur géométrique, le fractocentre®.
L’interaction de ces deux règles définit une dynamique de croissance hiérarchisée, que la suite a(n)a(n)a(n) encode intégralement.

Jean-Louis Lascoux – Bordeaux – 2025/08/02

[1] Diogène Laërce, Vies et doctrines des philosophes illustres, Livre VIII, §12. ____
Télécharger le document intégral avec en + les éléments mathématiques et géométriques (PDF) : A386761 : une suite géométrique issue de la subdivision tétraédrique d’un octaèdre régulier A386821 : Total tetrahedra in bifractal subdivision of stella octangula  
 
Par Actualités Médiation, Management & Gouvernance, Mathématiques & Géométrie, Physique
Lire la suite...
01Août

Une suite géométrique issue de la subdivision tétraédrique d’un octaèdre régulier

Introduction

Parmi les nombreuses façons de générer des suites d’entiers à partir de constructions géométriques, certaines se distinguent par leur simplicité formelle et leur richesse structurante. La nouvelle suite : Number of tetrahedra formed by iterative 4-ary subdivision of a regular stellar bitetrahedron (Stella Octangula configuration), starting from 8 initial tetrahedra est de celles-là.

Elle émerge d’un processus élémentaire et pourtant puissamment combinatoire :

subdiviser récursivement un ensemble de tétraèdres dans l’espace à partir d’un octaèdre régulier.

Décomposition initiale : de l’octaèdre au Stella Octangula

Considérons un octaèdre régulier, polyèdre de Platon à 8 faces triangulaires. En disposant deux tétraèdres réguliers emboîtés dans un cube (symétriquement opposés), on forme la Stella Octangula : une étoile géométrique dont l’intersection forme un octaèdre central.

Cet octaèdre peut être décomposé en 8 tétraèdres réguliers identiques, chacun occupant une portion symétrique de l’espace. Cette configuration initiale fournit le point de départ :

a(1)=8a(1) = 8

Subdivision récursive 4-aire

À chaque étape suivante, on applique la règle suivante :

Chaque tétraèdre est subdivisé en 4 tétraèdres plus petits, congruents au sein du volume initial.

Ce processus est récursif, homogène et volume-remplissant :

  • Tous les tétraèdres générés à un niveau n sont subdivisés à l’identique au niveau n+1,

  • Aucun chevauchement, aucune lacune : le volume global est conservé,

  • La symétrie octaédrique est préservée à chaque étape.

 

La nouvelle suite

Le nombre total de tétraèdres après n étapes est donné par la formule fermée :

a(n)=8(4n−1)3,n≥1a(n) = \frac{8(4^n - 1)}{3}, \quad n \geq 1

Les premiers termes sont :

python-repl
a(1) = 8 a(2) = 40 a(3) = 168 a(4) = 680 a(5) = 2728 ...

La récurrence vérifiée par cette suite est :

a(n)=5a(n−1)−4a(n−2),n≥3a(n) = 5a(n-1) - 4a(n-2), \quad n \geq 3

Et plus directement :

a(n)=a(n−1)+8⋅4n−1a(n) = a(n-1) + 8 \cdot 4^{n-1}

Chaque étape ajoute 8 fois plus de tétraèdres que celle d’avant à l’ordre n-1, ce qui traduit une croissance exponentielle strictement contrôlée.

Interprétation fractale

Ce processus produit une structure fractale tridimensionnelle, analogue en 3D à ce que représente le tapis de Sierpiński en 2D.

La fractale :

  • Est auto-similaire à chaque étape,

  • Suit un schéma de subdivision régulier et affine,

  • Conserve l'intégrité du volume global à toute profondeur.

Il s’agit donc d’un fractal de remplissage, et non d’un fractal lacunaire.

Propriétés géométriques

Propriété Valeur
Structure initiale 8 tétraèdres réguliers dans un octaèdre
Type de subdivision 4-aire (chaque tétraèdre → 4 tétraèdres)
Facteur de croissance local ×4
Facteur de croissance global ×5 – 4 (récurrence linéaire homogène d'ordre 2)
Dimension fractale D = log(4)/log(2) = 2
Applications potentielles Maillages, modélisation fractale, géométrie 3D

Comparaisons

Cette suite est numériquement liée à la suite classique :

A002450(n)=4n−13A002450(n) = \frac{4^n - 1}{3}

Mais elle s’en distingue :

  • par son origine géométrique canonique (le facteur 8 est imposé par la structure initiale),

  • par son rôle de modélisation spatiale réelle,

  • par ses applications spécifiques en 3D (infographie, simulation physique, structures hiérarchiques).

Potentiels

  • Maillages adaptatifs 3D : chaque subdivision affine le maillage de façon uniforme, sans compromettre la topologie.

  • Fractales tridimensionnelles : le modèle génère une structure pleinement volumique, auto-similaire.

  • Cristallographie théorique : certaines structures atomiques peuvent être modélisées par des emboîtements de tétraèdres.

  • Visualisation pédagogique : outil idéal pour introduire la notion de fractale 3D concrète.

Conclusion

La suite en cours de proposition sur l'encyclopédie OEIS est plus qu’une simple formule :
elle représente un objet géométrique canonique, structurant, doté d’une cohérence interne forte, d’une lien explicite avec les solides réguliers et d’un potentiel transdisciplinaire manifeste.

Elle incarne la jonction entre forme, nombre et récursion, dans un cadre purement tridimensionnel.

Par Mathématiques & Géométrie
Lire la suite...
28Juil

Fractale de la stella octangula, un bi-tétraèdre stellaire : nouvelle séquence mathématique issue de la géométrie 3D

Introduction

En explorant les propriétés géométriques des tétraèdres réguliers, dont j'utilise les principes systémiques dans le cadre du développement de l'ingénierie systémique relationnelle, pour assurer l'harmonie conceptuelle, avec un équilibre méthodologique des raisonnements, j'ai développé un nouveau concept. Celui-ci met en regard deux tétraèdres réguliers susceptibles de se former en Stella Octangula - cette élégante étoile à huit branches formée par l'interpénétration de deux tétraèdres réguliers. Par delà la symbolique que peut représenter cette configuration que j'ai nommé Bi-Tétraèdre Stellaire, j'ai en fait découvert une structure fractale remarquable qui ouvre des perspectives sur les séquences mathématiques.

L'observation

La Stella Octangula est connue au moins depuis la Renaissance. Lorsqu'on la décompose par ce que l'on perçoit immédiatement, on identifie 8 tétraèdres externes et l'œuf central est un octaèdre. Ainsi, ce n'est qu'un début : cette décomposition n'est pas seulement géométrique - elle est le point de départ d'un processus fractal infini.

Un processus de subdivision volumique

À partir des 8 tétraèdres initiaux, on peut appliquer une subdivision récursive :

  1. Étape 1 : 8 tétraèdres (décomposition initiale)
  2. Étape 2 : Chaque tétraèdre se divise en 4 → 8 + 32 = 40 tétraèdres
  3. Étape 3 : Les 32 nouveaux se divisent → 40 + 128 = 168 tétraèdres
  4. Étape 4 : 168 + 512 = 680 tétraèdres

Une formule mathématique

Cette croissance suit une loi précise :

a(n) = 8 × (4ⁿ - 1) / 3

où n représente le nombre d'étapes de subdivision.

Une Séquence : OEIS

Les premiers termes de cette séquence sont :

8, 40, 168, 680, 2728, 10920, 43688, 174760, 699048, 2796200...

Des propriétés remarquables

  • Croissance exponentielle : facteur 4 à chaque étape
  • Structure fractale : auto-similarité à toutes les échelles
  • Symétrie octaédrique : héritée de la configuration initiale

Visualisation

Applications et Perspectives

Cette séquence trouve des applications potentielles en :

  • Géométrie computationnelle : maillages tétraédriques adaptatifs
  • Cristallographie : modélisation de structures complexes
  • Fractales 3D : nouvelle famille de fractales volumiques

Code de Génération

Pour les intéressés, voici comment générer les termes de cette séquence (Python) :

def stella_bitetrahedra(n): """Nombre total de tétraèdres après n subdivisions récursives 4-aires, en partant de 8 tétraèdres initiaux issus de la Stella Octangula.""" return 8 * (4**n - 1) // 3

# Afficher les 10 premiers termes for i in range(1, 11): print(f"a({i}) = {stella_bitetrahedra(i)}")

Et après ?

Cette découverte illustre comment des structures géométriques classiques peuvent encore révéler des propriétés mathématiques inédites. La stella octangula, étudiée depuis des siècles, a désormais un compagnon qui offre déjà une vaste richesse structurelle... Un ensemble de formules sont dans le tuyau pour enrichir ce travail qui ne va pas aller sans surprendre par ses perspectives...
Par Articles, Curiosité, Mathématiques & Géométrie, News, Physique
Lire la suite...
25Mai

Les nombres premiers constants

Depuis des millénaires, les nombres premiers fascinent les mathématiciens. On les connaît comme les “briques” fondamentales des nombres entiers, indivisibles, essentiels en cryptographie, en théorie des nombres et dans l’histoire des mathématiques.
Mais une nouvelle classe vient aujourd’hui enrichir leur univers : les nombres premiers constants (base 8 et 10). Référencé sur le site OEIS

🔢 Qu’est-ce qu’un nombre premier constant ?

Prenez un nombre premier, par exemple 83. Additionnez ses chiffres : 8 + 3 = 11.
Additionnez encore les chiffres du résultat : 1 + 1 = 2.
À chaque étape, on continue à additionner les chiffres du nombre obtenu, jusqu’à arriver à un chiffre unique.

Ce processus est appelé réduction numérique ou somme digitale récursive.

👉 Un nombre premier constant est un nombre premier pour lequel toutes les étapes de cette réduction donnent encore des nombres premiers, jusqu’au chiffre final.

📍 Quelques exemples :

2, 3, 5, 7, 131, 311, 887

  • 131 → 1+ 3+1 = 5  ✔ (premier constant)

  • 311 → + 3 + 1 + 1 = 5 ✔ (premier constant)

  • 887 → 8 + 8 + 7 = 23 (premier) → 2 + 3 = 5 (premier constant)

🧠 Pourquoi est-ce intéressant ?

Les nombres premiers constants forment une famille nouvelle, définie par une propriété numérique interne.
Ils ne sont pas seulement premiers : ils sont stables lorsqu’on les "réduit" par leurs chiffres.
Cette stabilité numérique en fait des objets remarquables, à la frontière entre la mathématique pure, la symbolique et l’informatique.

🧪 Ma découverte

  • Il existe une infinité de nombres premiers constants, mais c'est encore plus intéressant d'observer un suite sur plusieurs bases. Ici, je n'ai pris que deux bases, mais j'ai déjà fait plusieurs observations sur un ensemble de bases. Et quoi ?

    • Leur comportement est régulier, prévisible dans certains cas, et profondément lié à des propriétés cachées des chiffres.

    • Ils pourraient jouer un rôle dans le codage numérique, la cryptographie, voire la modélisation de structures stables en intelligence artificielle.

📚 En résumé

Les nombres premiers constants sont comme des primes résilients :
même quand on les décompose par leurs chiffres,
ils continuent à rester premiers, à chaque étape.

Ils incarnent une nouvelle façon de regarder les nombres premiers, non plus seulement comme objets isolés, mais comme trajectoires stables dans l’univers des chiffres.

sur l'encyclopédie des nombres entiers oeis.org  

Par Articles, Curiosité, Divertissement, Mathématiques & Géométrie
Lire la suite...