Auteur - Jean-Louis Lascoux
16Sep

La médiation professionnelle, une approche neuroscientifique ?

Et si vous essayiez votre cerveau ?

À la croisée de la rigueur méthodologique et des dynamiques cérébrales, la médiation professionnelle s’impose comme un art de la raison appliquée aux relations humaines. Là où l’émotion domine, où l’incompréhension s’installe, elle trace un chemin structuré vers la clarification et l’ajustement des postures. Mais qu’est-ce qui la rend si puissante ? En plongeant au cœur des mécanismes neuronaux, nous découvrons une résonance inattendue : une méthode qui épouse les processus mêmes qui façonnent notre perception, notre régulation émotionnelle et nos décisions. Comprendre ces liens, c’est ouvrir la porte à une pratique renouvelée de la médiation, où chaque échange devient un levier de transformation.

Rationalité et cognition : un fondement scientifique de la médiation professionnelle

Pourquoi la médiation professionnelle permet-elle de résoudre des différends là où d'autres approches se heurtent à des blocages ? Si la question vaut d'être posée, ce n'est pas en comparant avec les autres méthodes que les vraies réponses se trouvent. Celles-ci se trouvent dans les avancées en neurosciences qui offrent aujourd'hui une opportunité scientifique pour comprendre pourquoi les techniques d'ingénierie systémique relationnelle® (ISR) appliquées en médiation professionnelle sont efficaces.

Un simple constat pourrait permettre de comprendre : la rationalité est le principe rigoureux de structuration de la méthodologie de l'ISR et c'est un phénomène si accessible et systémique du fonctionnement cérébral qu'il nous échappe lorsque la méthode nous fait défaut.

Puisque la communication est une construction cognitive, son organisation suit les mêmes principes de structuration que ceux qui régissent le fonctionnement cérébral. La médiation professionnelle est une pratique de la communication assistée par un tiers, le médiateur professionnel, ce n'est pas une méthode alternative de règlement des différends (Lascoux - 2017).

Mais le scepticisme quant à la rationalité est si fort que sa démonstration ne parvient pas à convaincre et des preuves multiples deviennent nécessaires pour emporter les convictions. Autrement dit, les résistances à la rationalité sont renforcées par des schémas cognitifs préexistants et des biais émotionnels. Et ce n'est pas toujours suffisant tellement la crédulité fait son lit dans les schémas cérébraux !

Ainsi, les principes de la médiation professionnelle ont une correspondance dans les dynamiques neuronales qui gouvernent les processus de prise de décision, de régulation émotionnelle et d'adaptation cognitive.

Plasticité cérébrale et adaptation

Le cerveau humain n'est pas figé dans ses représentations. Il révèle une plasticité constante (OCDE, 2007) qui lui permet d'ajuster ses schémas cognitifs et comportementaux en fonction de nouvelles expériences. Cette capacité est exploitée en médiation professionnelle pour accompagner les personnes dans la révision de leurs pensées limitantes et la reconstruction de leurs interactions relationnelles. Contrairement à une approche gestionnaire qui cherche à contenir le conflit par des implicites culturels et des compromis, la médiation professionnelle mobilise des processus cognitifs, par "l'élévation et la déclinaison conceptuelles", pour restructurer la dynamique relationnelle des parties impliquées, lesquels s'avèrent confortés par les observations de la plasticité cérébrale.

Même si certains blocages peuvent paraître échapper à la médiation professionnelle en raison d’influences externes, sa structuration cognitive reste un levier clé pour accompagner les parties et favoriser des ajustements relationnels. Aborder les mécanismes qui échappent à l'intentionnalité est une voie très opérationnelle.

Régulation des émotions et prise de décision

Le fonctionnement du cerveau repose sur un équilibre entre l'amygdale, centre de la régulation émotionnelle, et le cortex préfrontal, siège de l'analyse rationnelle. Lorsque les émotions prennent le dessus, les capacités de prise de recul et d'évaluation des conséquences sont altérées. Une posture exclusivement centrée sur la personne, caractéristique de l'altérocentrage, typique de la médiation professionnelle (Lascoux - 2017, 2019), favorise la mobilisation du cortex préfrontal, parce qu'elle engage un processus d'appropriation conceptuelle. L'échange entre le médiateur et son interlocuteur favorise un cheminement qui l'amène à dépasser ses réactions impulsives et de structurer sa prise de décision. L'identification des invariants de l'adversité, détaillés et analysés, permet d'interrompre les boucles répétitives d'entêtement, lesquelles sont souvent renforcées par les approches fondées sur les modèles de 'gestion des conflits' et de négociation priorisant les enjeux et les intérêts, au détriment des révisions de positionnements. Contrairement à la méthode de négociation dite 'raisonnée' (raisonnable - cf. la méthode de Roger Fisher et William Ury), il est essentiel de recentrer l'approche sur les positionnements eux-mêmes, plutôt que de privilégier les intérêts apparemment en présence.

La médiation professionnelle a-t-elle des limites ?

Si la médiation professionnelle repose sur des principes fondés sur l’usage de la raison, certaines situations de conflit présentent des imbrications relationnelles qui peuvent compliquer la dynamique de résolution. C’est notamment le cas lorsque des acteurs multiples, bien qu’invisibles dans l’échange direct, influencent lourdement les positions des parties en présence.

Ce type de situation se retrouve dans les conflits internationaux où des dirigeants politiques ou économiques externes sont impliqués. Les décisions prises en apparence sur des bases rationnelles peuvent être, en réalité, contraintes par des obligations tacites qui grèvent toute marge de négociation réelle. La corruption est la principale cause de la dénaturation du processus. Les protagonistes ne sont parfois même pas en capacité d’envisager une réflexion sur les fondements de leur posture, sinon par des arguments contradictoires et toujours dans la surenchère, sans crédibilité. Ce type de comportement n'est pas facile à restituer par le médiateur qui se trouve confronté à des manifestations ostentatoires de légitimité. Ici, il peut sembler que seul le temps puisse permettre de venir à bout du différend, or, c'est la difficulté de l'identification des facteurs des conflits. Dans ces situations, la capacité du médiateur (son audace !) à restituer les facteurs bloquants devient déterminante.

Dans ces situations, la médiation professionnelle peut être entravée non par une absence de rationalité des parties directement concernées, mais par l’existence de jeux d’acteurs externes qui conditionnent en amont les décisions et verrouillent les évolutions possibles. L’accompagnement des individus reste possible et pertinent, mais il ne saurait suffire à lui seul à déconstruire des mécaniques de blocage qui sont entretenues par des acteurs tiers, absents du processus de médiation. Dans tous les cas, c'est le développement des compétences du médiateur, éventuellement assisté par une équipe de supervision, qui doit être interrogé. De fait, avec moins de 30 ans d'existence, la pratique méthodologique est récente et l'expertise est en actualisation permanente ; cette mise en parallèle avec les neurosciences en est une démonstration.

Un modèle fondé sur la logique des interactions

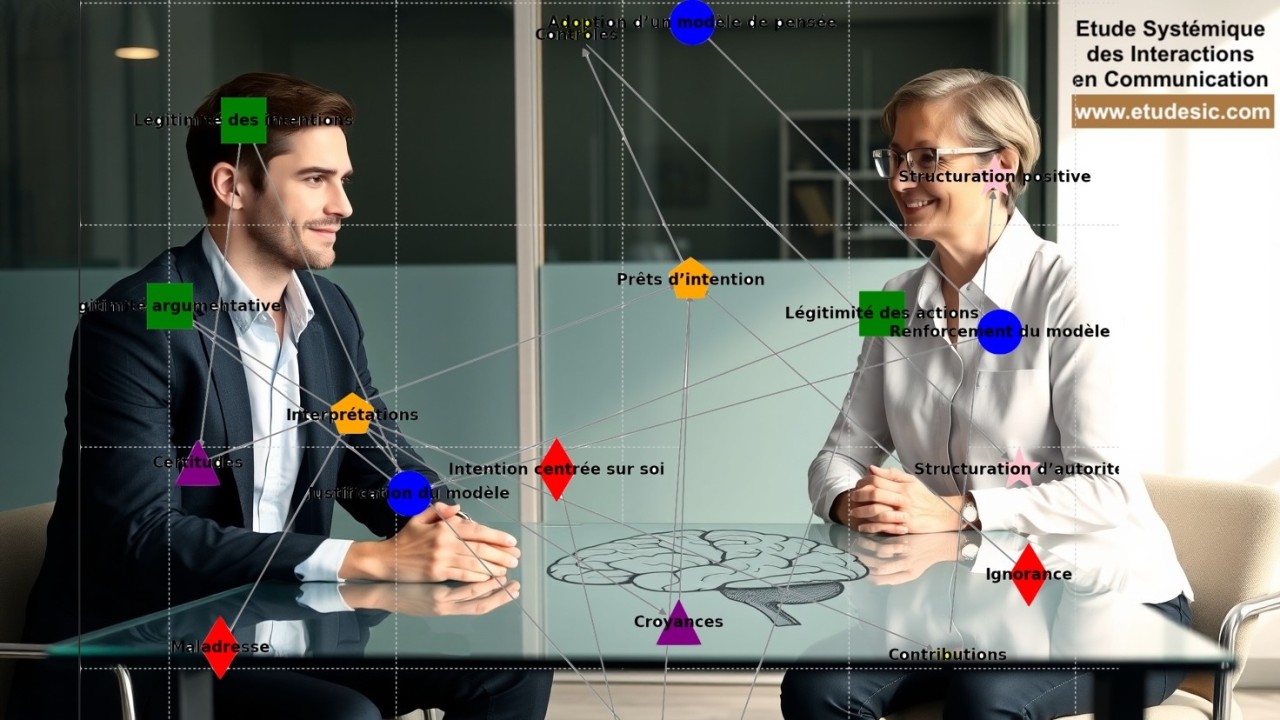
L'ingénierie systémique relationnelle®, appliquée en médiation professionnelle, repose sur une analyse précise des interactions humaines. Elle ne se contente pas d'encadrer les discussions, mais s'appuie sur des principes rigoureux qui facilitent l'émergence de solutions durables. Le modèle systémique des interactions en communication permet d'identifier les freins neuronaux à la coopération, favorisant ainsi une approche rationnelle des différends. Cette démarche s'inscrit dans une perspective scientifique où la compréhension du fonctionnement cérébral devient un levier essentiel pour transformer les conflits et promouvoir l'entente sociale.

Il est possible de comprendre ce qui se passe dans le cerveau d'une personne lorsqu'elle énonce ce qui est créateur de son adversité de la part de la partie adverse, et aussi lorsqu'elle comprend ce qui de sa part peut générer la conflictualité de la part de l'autre. Cette prise de conscience repose sur des ajustements neuronaux où l'activité du cortex préfrontal intervient pour analyser, structurer et apaiser les perceptions initiales.

Comprendre ce qui alimente l’adversité, et ce qui dans notre propre posture peut générer du conflit, est un travail qui mobilise des ajustements neuronaux précis. Ces ajustements sont soutenus par plusieurs neurotransmetteurs clés :

  • dopamine : facilite la réévaluation cognitive et la motivation à adopter de nouvelles stratégies.
  • sérotonine : stabilise les émotions et réduit les biais négatifs.
  • ocytocine : favorise la confiance et l’ouverture à l’autre.

Avec les mécanismes activés, c'est une meilleure régulation cognitive et émotionnelle qui ouvre la voie à des réajustements des dynamiques conflictuelles - dont la durabilité reste circonstancielle.

L’intégration de ces données par le cerveau favorise un ajustement progressif des réponses cognitives et émotionnelles, permettant ainsi une meilleure régulation des émotions.

Corrélation entre les réponses émotionnelles et la régulation cognitive en médiation professionnelle

Les réponses en situation de conflit sont liées aux mécanismes neurocognitifs qui sous-tendent la prise de décision et la régulation comportementale. En ingénierie systémique relationnelle (Lascoux - 2017, 2019), les Prêts d’Intention Négative (PIC), Interprétations jugeantes et Contraintes, lorsqu’ils s’accumulent, génèrent un phénomène de surenchère (S3), amplifiant les réactions émotionnelles et réduisant la flexibilité cognitive.

D’un point de vue neuroscientifique, ces dynamiques émotionnelles négatives sont associées à une activation excessive de l’amygdale, structure impliquée dans la détection des menaces et la régulation des réponses défensives (LeDoux, 1996). Une hyperactivation de l’amygdale est corrélée à une diminution des capacités de raisonnement et à une rigidité cognitive accrue (Etkin, Egner & Kalisch, 2011), ce qui se croise aisément avec les phénomènes d'entêtemlent typique de la conflictualité.

À l’inverse, le cortex préfrontal dorsolatéral (CPFDL) joue un rôle fondamental dans l’évaluation rationnelle des situations et le contrôle des impulsions émotionnelles (Miller & Cohen, 2001). Une activation plus marquée du CPFDL est associée à une meilleure régulation émotionnelle, ce que la pratique de la reconnaissance ne peut que produire favorablement, pour la prise de recul et l’élaboration d'une disposition adaptée pour faire baisser la tension.

L’hypothèse centrale est donc que l’intervention méthodologique du médiateur professionnel, par un processus structuré de restitution de sens et d’altérocentrage, permettrait à la fois :

  • une réduction de l’activation de l’amygdale en réponse aux stimuli conflictuels, limitant les réactions impulsives et défensives.
  • une augmentation de l’activation du cortex préfrontal dorsolatéral, facilitant une restructuration cognitive et une prise de décision rationnelle en contexte de conflit.

Cette hypothèse est soutenue par les travaux de Bogdan Draganski sur la plasticité cérébrale, qui ont démontré que des pratiques cognitives soutenues, comme la médiation et la régulation des interactions, peuvent induire des modifications structurelles du cortex préfrontal et améliorer les capacités de gestion émotionnelle (Draganski et al., 2004).

Ainsi, en rétablissant un équilibre fonctionnel entre les structures limbiques et les régions préfrontales, la médiation professionnelle apparaît comme une approche méthodologique susceptible de transformer les dynamiques de conflit en opportunités de réorganisation cognitive et relationnelle.

Ainsi, loin d'être une approche intuitive ou purement empirique, la médiation professionnelle s'impose comme une discipline fondée sur la rationalité du fonctionnement cérébral. Elle repose sur des principes scientifiques qui lui confèrent une efficacité objectivable, en résonance avec les dernières avancées en neurosciences. La prise en compte de la neuroplasticité et de la dynamique régulative du cerveau offre une explication à son succès, tout en ouvrant de nouvelles perspectives pour l'accompagnement des individus en situation de conflit.

Ces observations sont de nature à nous permettre d'envisager une tout autre théorie sur le fonctionnement cérébral que celles qui tendent à faire autorité actuellement. Et c'est à partir de cette approche que nous pouvons entrevoir de nouvelles perspectives de recherche et d'innovation, questionner les paradigmes établis. nous pouvons déjà envisager des applications inédites en matière de relations interpersonnelles, sociales, de management et de gouvernance, voire dans le champ des technologies de communication. La profession de médiateur, formée avec les techniques d'ingénierie relationnelle, fait sortir la médiation de ses improvisations hasardeuses. Il résulte de cette étude une forte invitation à s'approprier les techniques de la médiation professionnelle.

Mots clés : Adaptation cognitive, Amygdale, Altérocentrage, Conflit, Contraintes, Cortex préfrontal, Décision, Dynamique relationnelle, Entente sociale, Gouvernance, Ingénierie systémique relationnelle (ISR), Interaction humaine, Interprétations, Médiation professionnelle, Modèle systémique, Neuroplasticité, Neurosciences, PIC-, Plasticité cérébrale, Prêts d’Intention Négative, Processus cognitif, Régulation émotionnelle, Rationalité, Surenchère

Références

  • The Emotional Brain. Simon & Schuster. LeDoux, J. 1996
  • An Integrative Theory of Prefrontal Cortex Function. Annual Review of Neuroscience, 24(1), 167-202. E. K. Miller & J. D. Cohen 2001
  • Changes in grey matter induced by training—new insights from a longitudinal study using MRI. Nature Neuroscience, 6(8), 844-846, B. Draganski, C. Gaser, V. Busch, G. Schuierer, U. Bogdahn, & A. May, 2004.
  • Comprendre le cerveau : naissance d’une science de l’apprentissage, OCDE, Wu Ting-Fang (2007)
  • Plasticité fonctionnelle du cerveau et apprentissage moteur, medecinesciences.org, coordonné par Julien Doyon (2011)
  • Neurosciences et éducation, dossier coordonné par Pascale Toscani et Sylvain Connac, 2018
  • Emotional regulation and the neural bases of anxiety. Nature Reviews Neuroscience, 12(4), 223-231. Etkin, A., Egner, T., & Kalisch, R. 2011
  • Pratique de la Médiation professionnelle. Lascoux J-L. ESF, 2017
  • Dictionnaire de la médiation. Lascoux J-L. ESF, 2019
Par Articles, Neurosciences
Lire la suite...
06Sep

Ces années que nos horloges numériques ne montreront jamais / These Years That Our Digital Clocks Will Never Show

Le hasard des lectures numériques réserve parfois des paradoxes temporels et met en évidence des conceptions culturelles de la relation au temps. Partons d’une expérience de pensée simple…

The randomness of digital readings sometimes reveals temporal paradoxes and highlights cultural conceptions of our relationship with time. Let us start with a simple thought experiment…

Une observation anodine / An Ordinary Observation

Il est 19:57 (format 24 h, usage courant en Europe). En jetant un coup d’œil à mon téléphone, mon esprit fait un saut dans le temps : je lis « 1957 ». A ce moment, je sais que ce n’est pas le réel qui s’affiche, mais une convention qui me projette son récit. Me vient alors une question en apparence triviale — toutes les années peuvent-elles s’afficher sur un cadran au format 24 h ?

Réponse : non. Pas plus que pour tous les autres formats.

It is 19:57 (24-hour format, common usage in Europe). Glancing at my phone, my mind makes a leap through time: I read "1957". At this moment, I know that what is displayed is not reality, but a convention projecting its narrative to me. A seemingly trivial question then comes to mind—can all years be displayed on a 24-hour format clock face?

Answer: no. No more than for any other formats.

De l’analogie à la règle / From Analogy to Rule

Une horloge numérique affiche HH:MM (heures : minutes). Pour qu’une année ABCD (AB = deux premiers chiffres, CD = deux derniers) se lise comme une heure valide, deux conditions strictes s’imposent :

  • Heures : AB ∈ [00, 23]
  • Minutes : CD ∈ [00, 59]

Condition d’affichabilité : une année est « affichable » si et seulement si AB ∈ [00, 23] et CD ∈ [00, 59].

A digital clock displays HH:MM (hours:minutes). For a year ABCD (AB = first two digits, CD = last two) to be read as a valid time, two strict conditions must be met:

  • Hours: AB ∈ [00, 23]
  • Minutes: CD ∈ [00, 59]

Displayability condition: a year is "displayable" if and only if AB ∈ [00, 23] and CD ∈ [00, 59].

Application et exemples

Années valides

  • 1957 → AB = 19 (≤ 23), CD = 57 (≤ 59)
  • 2024 → AB = 20 (≤ 23), CD = 24 (≤ 59)
  • 2359 → AB = 23 (≤ 23), CD = 59 (≤ 59) → dernière année valide
  • 0001 → AB = 00 (≤ 23), CD = 01 (≤ 59)

Années invalides

  • 1960 → CD = 60 (> 59) → impossible (après 19:59 vient 20:00)
  • 1999 → CD = 99 (> 59)
  • 2400 → AB = 24 (> 23) → impossible (après 23:59 vient 00:00)

Note : 2024 est une année valide et 20:24 une heure valide. L’illusion de son « impossibilité » vient d’une confusion avec le passage de siècle ; le critère est purement numérique.

Quantification du phénomène (0000 à 9999)*

  • Minutes invalides : pour chaque AB ∈ [00, 23], 40 valeurs interdites de CD (60–99).
    → 24 × 40 = 960 années invalides.
  • Heures invalides : toute année ≥ 2400 est invalide.
    → de 2400 à 9999 inclus = 7 600 années invalides.

Total invalides = 960 + 7 600 = 8 560 années.
Total valides = 10 000 – 8 560 = 1 440 années.

* Convention purement numérique : intervalle 0000–9999, indépendamment des calendriers historiques.

Visualisation

PériodeStatutConditionExemplesNombre
0000–2399InvalidesCD ≥ 600060–0099, …, 2360–2399960
2400–9999InvalidesAB ≥ 242400, 2401, …, 99997 600
0000–2359ValidesAB ∈ [00,23], CD ∈ [00,59]0000–0059, …, 2300–23591 440
Total———10 000

Le filtre temporel de l’horloge / The Clock's Temporal Filter

Notre manière de compter les heures impose un filtre numérique : seules 1 440 années sur 10 000 (soit 14,4 %) peuvent apparaître comme une heure valide sur un cadran 24 h.

La prochaine fois que vous verrez 20:59, pensez que 2059 fait partie de ce club restreint des années qui coïncident, même brièvement, avec une heure réelle de la journée.

Our way of counting hours imposes a numerical filter: only 1,440 years out of 10,000 (or 14.4%) can appear as a valid time on a 24-hour clock face.

The next time you see 20:59, think that 2059 is part of this restricted club of years that coincide, however briefly, with a real time of day.

Du calcul à l’interprétation

Sur le plan strictement numérique, la règle est claire :

Une année ABCD est affichable si et seulement si AB ∈ [00, 23] et CD ∈ [00, 59].
Cela représente 14,4 % des années (1 440 sur 10 000). La dernière année affichable est 2359.

Ce résultat nous rappelle que le temps que nous lisons n’est pas une donnée brute de la réalité, mais une convention. Changer de format (24 h ↔ 12 h, lecture gauche ↔ droite) change ce qui est « possible » d’afficher. Autrement dit, la manière de chiffrer nos cadrans conditionne la perception que nous avons du temps.

De la convention à la perception / From Convention to Perception

À 19:59, il suffit d’une minute pour passer à 20:00 : ce saut peut se lire comme une image — une sorte de « saut quantique » métaphorique. En un instant, on a basculé de 1959 à 2000, comme si l’horloge compressait 40 ans en un battement numérique.

Le temps est une fable de cadran : notre perception suit la convention, et la convention oriente nos croyances.

  • Avec un découpage en 24 heures, on se sent inscrit dans une continuité linéaire.
  • Avec un découpage en deux cycles de 12 heures, certains auront l’impression de disposer d’un temps plus écourté nécessitant plus d’empressement.

Ainsi, le temps que nous mesurons est d’abord un temps que nous racontons. Les chiffres filtrent nos expériences, et chaque convention d’affichage devient une mise en scène culturelle du temps qui dépend, non pas de la réalité du moment, mais de ceux qui la tissent après coup.

At 19:59, it takes just one minute to reach 20:00: this jump can be read as an image—a sort of metaphorical "quantum leap". In an instant, we have jumped from 1959 to 2000, as if the clock compressed 40 years into a digital beat.

Time is a fable of the clock face: our perception follows convention, and convention guides our beliefs.

  • With a 24-hour division, we feel inscribed in a linear continuity.
  • With a division into two 12-hour cycles, some will have the impression of having more limited time requiring more urgency.

Thus, the time we measure is first and foremost a time we narrate. Numbers filter our experiences, and each display convention becomes a cultural staging of time that depends, not on the reality of the moment, but on those who weave it after the fact.

Par Mathématiques & Géométrie
Lire la suite...
02Août

A Bifractal Integer Sequence from Recursive Subdivision of the Stella Octangula

Croissance bifractale tétraédrique : une suite entière dérivée de la subdivision récursive de la Stella Octangula

Fractale stella octangula : une suite géométrique bifractale à potentiel théorique et industriel

Introduction philosophique

La manière dont nous voyons le monde conditionne profondément la manière dont nous le vivons. Cela peut sembler paradoxal, voire non académique, de commencer une étude mathématique par une réflexion d’ordre philosophique. Tant pis. Je n’ai pas été formé par les voies académiques traditionnelles : je suis autodidacte — en tout, y compris dans ce que j’appelle le tourisme existentiel. Certaines visions du monde projettent partout des arrondis, des courbes lissées, comme si adoucir les contours était la voie naturelle vers l’harmonie. C’est une illusion. Il n’y a rien de plus complexe, ni de plus exigeant, que d’arrondir véritablement les angles. Car ce geste — en apparence simple — exige un ajustement précis entre des éléments dissemblables, une gestion des tensions, et une tendance à négocier les points de rupture. On y retrouve les fondements des modèles de pensée économiques, administratifs, managériaux, avec tout le lexique qui les façonnent. C’est à partir de cette relecture fondatrice entre angle et arrondi, entre structure et adaptation, que je propose ici une approche bifractale : géométrique dans sa forme, mathématique dans son expression, philosophique dans sa visée.
Définie en 1509 par Luca Pacioli dans son traité De Divina Proportione, l’objet dont le nom de Stella Octangula sera donné par Johannes Kepler, est initialement pensée comme un symbole de proportion divine, dans l’esprit néoplatonicien de la Renaissance. Les illustrations de Léonard de Vinci lui confèrent un statut emblématique d’harmonie géométrique incarnée. Elle est redécouverte en 1609 par Johannes Kepler, qui y voit une forme parfaite, résultant de l’interpénétration de deux tétraèdres réguliers inversés. Plus tard, Leonhard Euler (1707–1783) formule la relation topologique fondamentale V−E+F=2, marquant une étape décisive dans la formalisation des structures closes. Ce progrès, en apparence neutre, tend paradoxalement à enfermer la Stella Octangula dans une lecture statique et figée. Ma proposition s’inscrit dans une tout autre logique : réouvrir la figure vers des perspectives dynamiques et systémiques, en la réinscrivant dans le champ des fractales, concept introduit dans les années 1970 par Benoît Mandelbrot. L’application bifractale présentée ici vise à détacher la Stella Octangula de sa clôture topologique traditionnelle, pour en faire le support d’une croissance récursive ajustative, à la fois volumique (8-aire) et planaire (4-aire). C’est cette réinterprétation structurelle qui justifie mon choix de l’appeler désormais Bi-Tétraèdre Stellaire : ·       une appellation qui insiste sur son potentiel combinatoire, ·       sa dynamique de subdivision (organisée autour d’un Fractocentre®, et non d’un barycentre académique), ·       et sa capacité de déploiement hiérarchisé dans des modèles fractals d’ingénierie. Il ne s’agit plus d’un simple objet géométrique : c’est un modèle opératif, à la croisée de la précision mathématique, de la complexité fractale, et d’une visée systémique ajustative.
Dans cette recherche, la Stella Octangula– sur laquelle je reviens en nommant la structure « Bi-Tétraèdre stellaire », devient plus qu’un objet de curiosité géométrique : elle s’impose comme une autre forme de pensée. En effet, formée par l’interpénétration parfaite de deux tétraèdres opposés, elle incarne une tension équilibrée entre dualité et symétrie, entre stabilité et expansion. Ce n’est pas tant la figure elle-même qui importe, que la manière dont elle peut être subdivisée, régénérée, complexifiée — sans jamais perdre son principe d’organisation, avec une tonalité nouvelle associée à la liberté. Ce processus de subdivision, je le nomme ici bifractale, parce qu’il repose sur deux lois de croissance distinctes mais coordonnées. L’une est volumique, l’autre est planaire ; l’une s’appuie sur la démultiplication, l’autre sur la structuration. Ensemble, elles génèrent une dynamique hiérarchique d’une remarquable cohérence. Mais pourquoi s’y intéresser ? Parce qu’en modélisant cette croissance, en l’analysant sous forme d’une suite entière bien définie, nous accédons à plus qu’un simple jeu de nombres. Nous touchons à un modèle opératif d’ajustement. Un modèle qui relie le discret et le continu, le local et le global, l’ordre mathématique et la plasticité du réel. Ce lien entre pensée, structure et ajustement n’est pas nouveau. Il remonte à Pythagore, souvent considéré comme l’inventeur du mot philosophie – philo-sophia, l’amour de la sagesse. D’après Diogène Laërce[1], Pythagore aurait introduit ce terme pour désigner une posture de recherche désintéressée, tournée vers l’harmonie des lois universelles. Mais il ne s’agissait pas d’une sagesse vague ou contemplative : pour Pythagore, cette quête passait nécessairement par les nombres, les figures, les rapports. C’est à travers le langage mathématique et géométrique qu’il percevait l’ordre caché du cosmos, et c’est à travers cette exigence qu’il fondait une discipline intérieure. Revenir à la Stella Octangula, Bi-Tétraèdre Stellaire, avec une attention moderne, combinatoire, algorithmique, n’est donc pas un détournement du sens philosophique initial. C’est, au contraire, une fidélité profonde à l’idée pythagoricienne d’une sagesse en actes, qui cherche à comprendre le monde en le structurant — non pour le simplifier, mais pour mieux épouser sa complexité. C’est ainsi que j’ai développé un ensemble théorico-pratique qui touche à la fois au fonctionnement personnel (la théorie du cerveau corrélatif et de l’harmonisation ajustative (TCC-HA), la théorie de l’ajustativité temporelle (T.AJT), les deux réunies en Théorie de l’Ajustativité Générale (#TAG). C’est ambitieux, j’en conviens. Pour autant, cette approche est cohérente et se retrouve opérationnelle, en premier lieu, dans les contextes relationnels humains, puisque c’est là que j’ai développé la première application de mon modèle géométrique, la médiation professionnelle, la profession de médiateur fondée sur la qualité relationnelle et l’Ingénierie Systémique Relationnelle®. À partir de cette articulation entre structure géométrique, dynamique d’ajustement et modélisation relationnelle, nous pouvons formuler une expression mathématique rigoureuse de la croissance bifractale associée à la Stella Octangula. Cette modélisation conduit naturellement à une suite entière a(n), dont chaque terme représente le nombre total de tétraèdres présents à l’itération n d’un processus récursif de subdivision. Ce processus repose sur deux lois complémentaires :
  • une subdivision volumique 8-aire, appliquée aux tétraèdres externes de la structure ;
  • une subdivision planaire 4-aire, centrée sur le cœur géométrique, le fractocentre®.
L’interaction de ces deux règles définit une dynamique de croissance hiérarchisée, que la suite a(n)a(n)a(n) encode intégralement.

Jean-Louis Lascoux – Bordeaux – 2025/08/02

[1] Diogène Laërce, Vies et doctrines des philosophes illustres, Livre VIII, §12. ____
Télécharger le document intégral avec en + les éléments mathématiques et géométriques (PDF) : A386761 : une suite géométrique issue de la subdivision tétraédrique d’un octaèdre régulier A386821 : Total tetrahedra in bifractal subdivision of stella octangula  
 
Par Mathématiques & Géométrie, Physique
Lire la suite...
01Août

Une suite géométrique issue de la subdivision tétraédrique d’un octaèdre régulier

Introduction

Parmi les nombreuses façons de générer des suites d’entiers à partir de constructions géométriques, certaines se distinguent par leur simplicité formelle et leur richesse structurante. La nouvelle suite : Number of tetrahedra formed by iterative 4-ary subdivision of a regular stellar bitetrahedron (Stella Octangula configuration), starting from 8 initial tetrahedra est de celles-là.

Elle émerge d’un processus élémentaire et pourtant puissamment combinatoire :

subdiviser récursivement un ensemble de tétraèdres dans l’espace à partir d’un octaèdre régulier.

Décomposition initiale : de l’octaèdre au Stella Octangula

Considérons un octaèdre régulier, polyèdre de Platon à 8 faces triangulaires. En disposant deux tétraèdres réguliers emboîtés dans un cube (symétriquement opposés), on forme la Stella Octangula : une étoile géométrique dont l’intersection forme un octaèdre central.

Cet octaèdre peut être décomposé en 8 tétraèdres réguliers identiques, chacun occupant une portion symétrique de l’espace. Cette configuration initiale fournit le point de départ :

a(1)=8a(1) = 8

Subdivision récursive 4-aire

À chaque étape suivante, on applique la règle suivante :

Chaque tétraèdre est subdivisé en 4 tétraèdres plus petits, congruents au sein du volume initial.

Ce processus est récursif, homogène et volume-remplissant :

  • Tous les tétraèdres générés à un niveau n sont subdivisés à l’identique au niveau n+1,

  • Aucun chevauchement, aucune lacune : le volume global est conservé,

  • La symétrie octaédrique est préservée à chaque étape.

 

La nouvelle suite

Le nombre total de tétraèdres après n étapes est donné par la formule fermée :

a(n)=8(4n−1)3,n≥1a(n) = \frac{8(4^n - 1)}{3}, \quad n \geq 1

Les premiers termes sont :

python-repl
a(1) = 8 a(2) = 40 a(3) = 168 a(4) = 680 a(5) = 2728 ...

La récurrence vérifiée par cette suite est :

a(n)=5a(n−1)−4a(n−2),n≥3a(n) = 5a(n-1) - 4a(n-2), \quad n \geq 3

Et plus directement :

a(n)=a(n−1)+8⋅4n−1a(n) = a(n-1) + 8 \cdot 4^{n-1}

Chaque étape ajoute 8 fois plus de tétraèdres que celle d’avant à l’ordre n-1, ce qui traduit une croissance exponentielle strictement contrôlée.

Interprétation fractale

Ce processus produit une structure fractale tridimensionnelle, analogue en 3D à ce que représente le tapis de Sierpiński en 2D.

La fractale :

  • Est auto-similaire à chaque étape,

  • Suit un schéma de subdivision régulier et affine,

  • Conserve l'intégrité du volume global à toute profondeur.

Il s’agit donc d’un fractal de remplissage, et non d’un fractal lacunaire.

Propriétés géométriques

Propriété Valeur
Structure initiale 8 tétraèdres réguliers dans un octaèdre
Type de subdivision 4-aire (chaque tétraèdre → 4 tétraèdres)
Facteur de croissance local ×4
Facteur de croissance global ×5 – 4 (récurrence linéaire homogène d'ordre 2)
Dimension fractale D = log(4)/log(2) = 2
Applications potentielles Maillages, modélisation fractale, géométrie 3D

Comparaisons

Cette suite est numériquement liée à la suite classique :

A002450(n)=4n−13A002450(n) = \frac{4^n - 1}{3}

Mais elle s’en distingue :

  • par son origine géométrique canonique (le facteur 8 est imposé par la structure initiale),

  • par son rôle de modélisation spatiale réelle,

  • par ses applications spécifiques en 3D (infographie, simulation physique, structures hiérarchiques).

Potentiels

  • Maillages adaptatifs 3D : chaque subdivision affine le maillage de façon uniforme, sans compromettre la topologie.

  • Fractales tridimensionnelles : le modèle génère une structure pleinement volumique, auto-similaire.

  • Cristallographie théorique : certaines structures atomiques peuvent être modélisées par des emboîtements de tétraèdres.

  • Visualisation pédagogique : outil idéal pour introduire la notion de fractale 3D concrète.

Conclusion

La suite en cours de proposition sur l'encyclopédie OEIS est plus qu’une simple formule :
elle représente un objet géométrique canonique, structurant, doté d’une cohérence interne forte, d’une lien explicite avec les solides réguliers et d’un potentiel transdisciplinaire manifeste.

Elle incarne la jonction entre forme, nombre et récursion, dans un cadre purement tridimensionnel.

Par Mathématiques & Géométrie
Lire la suite...
28Juil

Fractale de la stella octangula, un bi-tétraèdre stellaire : nouvelle séquence mathématique issue de la géométrie 3D

Introduction

En explorant les propriétés géométriques des tétraèdres réguliers, dont j'utilise les principes systémiques dans le cadre du développement de l'ingénierie systémique relationnelle, pour assurer l'harmonie conceptuelle, avec un équilibre méthodologique des raisonnements, j'ai développé un nouveau concept. Celui-ci met en regard deux tétraèdres réguliers susceptibles de se former en Stella Octangula - cette élégante étoile à huit branches formée par l'interpénétration de deux tétraèdres réguliers. Par delà la symbolique que peut représenter cette configuration que j'ai nommé Bi-Tétraèdre Stellaire, j'ai en fait découvert une structure fractale remarquable qui ouvre des perspectives sur les séquences mathématiques.

L'observation

La Stella Octangula est connue au moins depuis la Renaissance. Lorsqu'on la décompose par ce que l'on perçoit immédiatement, on identifie 8 tétraèdres externes et l'œuf central est un octaèdre. Ainsi, ce n'est qu'un début : cette décomposition n'est pas seulement géométrique - elle est le point de départ d'un processus fractal infini.

Un processus de subdivision volumique

À partir des 8 tétraèdres initiaux, on peut appliquer une subdivision récursive :

  1. Étape 1 : 8 tétraèdres (décomposition initiale)
  2. Étape 2 : Chaque tétraèdre se divise en 4 → 8 + 32 = 40 tétraèdres
  3. Étape 3 : Les 32 nouveaux se divisent → 40 + 128 = 168 tétraèdres
  4. Étape 4 : 168 + 512 = 680 tétraèdres

Une formule mathématique

Cette croissance suit une loi précise :

a(n) = 8 × (4ⁿ - 1) / 3

où n représente le nombre d'étapes de subdivision.

Une Séquence : OEIS

Les premiers termes de cette séquence sont :

8, 40, 168, 680, 2728, 10920, 43688, 174760, 699048, 2796200...

Des propriétés remarquables

  • Croissance exponentielle : facteur 4 à chaque étape
  • Structure fractale : auto-similarité à toutes les échelles
  • Symétrie octaédrique : héritée de la configuration initiale

Visualisation

Applications et Perspectives

Cette séquence trouve des applications potentielles en :

  • Géométrie computationnelle : maillages tétraédriques adaptatifs
  • Cristallographie : modélisation de structures complexes
  • Fractales 3D : nouvelle famille de fractales volumiques

Code de Génération

Pour les intéressés, voici comment générer les termes de cette séquence (Python) :

def stella_bitetrahedra(n): """Nombre total de tétraèdres après n subdivisions récursives 4-aires, en partant de 8 tétraèdres initiaux issus de la Stella Octangula.""" return 8 * (4**n - 1) // 3

# Afficher les 10 premiers termes for i in range(1, 11): print(f"a({i}) = {stella_bitetrahedra(i)}")

Et après ?

Cette découverte illustre comment des structures géométriques classiques peuvent encore révéler des propriétés mathématiques inédites. La stella octangula, étudiée depuis des siècles, a désormais un compagnon qui offre déjà une vaste richesse structurelle... Un ensemble de formules sont dans le tuyau pour enrichir ce travail qui ne va pas aller sans surprendre par ses perspectives...
Par Articles, Mathématiques & Géométrie, Physique
Lire la suite...
25Mai

Les nombres premiers constants

Depuis des millénaires, les nombres premiers fascinent les mathématiciens. On les connaît comme les “briques” fondamentales des nombres entiers, indivisibles, essentiels en cryptographie, en théorie des nombres et dans l’histoire des mathématiques.
Mais une nouvelle classe vient aujourd’hui enrichir leur univers : les nombres premiers constants (base 8 et 10). Référencé sur le site OEIS

🔢 Qu’est-ce qu’un nombre premier constant ?

Prenez un nombre premier, par exemple 83. Additionnez ses chiffres : 8 + 3 = 11.
Additionnez encore les chiffres du résultat : 1 + 1 = 2.
À chaque étape, on continue à additionner les chiffres du nombre obtenu, jusqu’à arriver à un chiffre unique.

Ce processus est appelé réduction numérique ou somme digitale récursive.

👉 Un nombre premier constant est un nombre premier pour lequel toutes les étapes de cette réduction donnent encore des nombres premiers, jusqu’au chiffre final.

📍 Quelques exemples :

2, 3, 5, 7, 131, 311, 887

  • 131 → 1+ 3+1 = 5  ✔ (premier constant)

  • 311 → + 3 + 1 + 1 = 5 ✔ (premier constant)

  • 887 → 8 + 8 + 7 = 23 (premier) → 2 + 3 = 5 (premier constant)

🧠 Pourquoi est-ce intéressant ?

Les nombres premiers constants forment une famille nouvelle, définie par une propriété numérique interne.
Ils ne sont pas seulement premiers : ils sont stables lorsqu’on les "réduit" par leurs chiffres.
Cette stabilité numérique en fait des objets remarquables, à la frontière entre la mathématique pure, la symbolique et l’informatique.

🧪 Ma découverte

  • Il existe une infinité de nombres premiers constants, mais c'est encore plus intéressant d'observer un suite sur plusieurs bases. Ici, je n'ai pris que deux bases, mais j'ai déjà fait plusieurs observations sur un ensemble de bases. Et quoi ?

    • Leur comportement est régulier, prévisible dans certains cas, et profondément lié à des propriétés cachées des chiffres.

    • Ils pourraient jouer un rôle dans le codage numérique, la cryptographie, voire la modélisation de structures stables en intelligence artificielle.

📚 En résumé

Les nombres premiers constants sont comme des primes résilients :
même quand on les décompose par leurs chiffres,
ils continuent à rester premiers, à chaque étape.

Ils incarnent une nouvelle façon de regarder les nombres premiers, non plus seulement comme objets isolés, mais comme trajectoires stables dans l’univers des chiffres.

sur l'encyclopédie des nombres entiers oeis.org  

Par Mathématiques & Géométrie
Lire la suite...
08Mai

Non, Poincaré, le monde ne tourne pas rond !

Bon, c'est vrai que c'est un peu facile, mais l'idée est là, dans l'humour du titre, très sérieusement. Hé oui, dans votre tête, la rondeur est rarement au rendez-vous, comme dans l'univers. Ca vous dit quelque chose cette expression : "Ca ne tourne pas rond dans sa tête !", qui sous-entend clairement que si ça tourne rond, alors, tout va bien.  Et si c'était une représentation infondée du monde ? De fait, la sphère peut paraître comme une forme parfaite. Pourtant, ce n'est pas très sûr. A y regarder d'un peu plus près, la sphère n'est pas aussi ronde que cela. Certes, elle paraît bien douce quand on la regarde dans une bulle. Elle nous entraîne dans le monde des mathématiques. A ce propos, vous connaissez la conjecture de Poincaré ? Il paraît que c'est l'un des grands mystères des mathématiques. Cette conjecture pose la question suivante : toute forme tridimensionnelle sans trou peut-elle être transformée en sphère ? Quelqu'un, en 2003, le mathématicien Grigori Perelman, a répondu oui. Pour cette affirmation, il s'est appuyé sur une méthode mathématique appelée "Ricci Flow" de Richard S. Hamilton.

Mais cette démonstration, bien qu’essentielle, ne dit rien sur la manière dont les formes réelles — celles que l’on observe dans la nature, dans les écosystèmes ou dans les structures sociales — s’organisent, se stabilisent ou s’ajustent.

C’est dans cette perspective que j'introduis un nouveau concept non mathématique au sens strict, mais opératif dans le cadre de la Théorie de l'Ajustativité Générale (TAG).

C’est là qu’intervient le concept de "fractosphéricité", un concept qui se conjugue avec la (TAG) que je développe en lien avec l'ingénierie systémique relationnelle®.

Définition du concept proposé

Fractosphéricité : propriété d’une forme tridimensionnelle simplement connexe (sans trou topologique), non sphérique, qui atteint néanmoins un état stable ou harmonieux dans un système complexe.

Autrement dit, une forme n’a pas besoin d’être sphérique pour être équilibrée. Certaines configurations fractales, polarisées, irrégulières — mais ajustées selon leur propre dynamique interne — peuvent manifester une stabilité comparable à celle d’une sphère.

Le modèle DT-FRACTAL®, issu de la TAG, explore précisément ces structures : des formes non sphériques, mais barycentriquement cohérentes, organisées par ajustement relationnel, et non par symétrie idéale.

Pourquoi cette approche est scientifique ?

Parce qu’elle ne rejette pas les théories antérieures (topologie classique, géométrie différentielle), mais les complète en proposant un nouvel angle de lecture pour les formes complexes observables.

La fractosphéricité introduit un cadre opératif d’analyse des formes ajustées dans les systèmes vivants, sociaux ou informationnels.

Ce que cela change

Cela ouvre une perspective nouvelle :

  • Un monde pas forcément centré, mais cohérent.
  • Un monde pas forcément symétrique, mais stabilisé par ajustement.
  • Une manière d’observer la réalité autrement, sans réduire l’harmonie à la perfection géométrique.
Donc : la fractosphéricité n'est pas une vérité mathématique à prouver comme un théorème, c'est une grille de lecture, un nouveau regard sur les formes de l'univers. Elle illustre comment la science peut avancer non pas en niant ce qui précède, mais en complétant les réponses par d'autres questions.
C'est ainsi que vous pouvez commencer à penser autrement.

Publication sur HAL.science :

Conjecture de Poincaré : au-delà de la sphère (Relecture ajustative)

 
Par Articles, Physique
Lire la suite...
07Mai

Karpman, un triangle qui joue de fausses notes relationnelles depuis trop longtemps

Après avoir déconstruit la pyramide de Maslow comme mythe psychosociologique issu d’un schéma hiérarchique figé, j’ouvre un nouveau chantier critique : le triangle dramatique de Karpman.

Maslow et Karpman ont imposé des repères. L’un comme l’autre sont devenus des références internalisées, enseignées, rarement questionnées. Ils séduisent par leur simplicité. Ils frappent par leur pouvoir narratif. Pourtant, ces modèles relèvent de la fiction intellectuelle. Mais ils enferment la pensée dans des schémas figés. Le triangle dramatique articule les rôles de Victime, Persécuteur et Sauveur. Il fige, suspecte, enferme. Il a assigné des millions d’individus à des postures aussi théâtrales que toxiques. Je vous propose d'en sortir. Je vous invite à repenser nos modèles. L'idée est de passer d’un imaginaire interprétatif à une logique d’ajustement. C'est possible de préférer la co-régulation vivante, en toute objectivité, à la répétition pathologique, qui reste une violente subjectivité sociale et interpersonnelle.

Sortir du triangle dramatique : au-delà du modèle victimaire

Introduction

Depuis les années 1990, le triangle dramatique a connu une diffusion massive en France. Il s’est imposé dans les milieux des risques psychosociaux (RPS) et de la prévention du harcèlement moral. Karpman s’inspire des contes et des scénarios quotidiens pour proposer une lecture simple des conflits : trois rôles récurrents, trois postures liées à des déséquilibres psychiques. Le modèle n’est pas nécessairement pathologique à l’origine. Mais il est lié à l'environnement où l'idée est de soigner le mental des individus et il s’inscrit dans la tradition culpabilisante de la psychologie occidentale. La culture psy dominante l’a figé. L'appropriation populaire et le modèle de pensée juridique l’a instrumentalisé et versé dans la moralisation. Ce triangle date de la même période que le modèle triangulaire de René Girard, avec le désir mimétique. L'auteur de Mensonge romantique et Vérité romanesque et de La Violence et le Sacré, conduit à la révélation ou au sacrifice. Comme Karpman, Girard pense la relation comme soumission à une force. Ce déterminisme relationnel a pesé sur les pratiques des thérapies, des accompagnements individuels et de la médiation traditionnelle. Il a renforcé des logiques d’accusation et de disqualification.

Un modèle interprété comme dramatisation et dissuasion

Le triangle dramatique peut servir à observer, mais il porte son travers d'usage : il sert à classer. Il est devenu un outil d’alerte comportementale. Chaque rôle a été surinterprété. La victime peut être considérée comme manipulatrice, le sauveur dominateur, le persécuteur pervers. Le modèle est mobilisé pour justifier des procédures, parfois jusqu’à l’exclusion. Cette dérive empêche la co-construction. Elle empêche la régulation. Elle installe la suspicion. Elle rigidifie la relation.

Un outil capté par les institutions : prévention, suspicion et disqualification

Les institutions ont intégré ce triangle dans leurs outils RPS. Il sert à détecter les rôles à risque. Il devient un prisme de lecture standardisé. La médiation qui en fait usage s’en trouve biaisée. L’intervention est justifiée par l’attribution de rôles figés. On perd de vue l’ajustement préconisée par l'ingénierie systémique relationnelel. On catégorise sans contextualiser. Cela génère de la défiance et de la désolidarisation.

Une médiation instrumentalisée et dépolitisée

Quand le triangle dramatique gouverne la lecture, la médiation devient un rituel. Elle ne permet plus une parole contributive. Elle valide une assignation. Elle cherche à neutraliser, non à ajuster. Ce n’est plus une recherche d’entente, mais une procédure d’endiguement. La logique du triangle produit un effet de gel. On maintient chacun dans un rôle. On efface la possibilité de transformation partagée.

La logique victimaire dans la loi française

Dans ce contexte, l’article L.1152-1 du Code du travail, promulgué en 2002, repose sur une conception asymétrique. La souffrance perçue légitime le déséquilibre. La plainte devient preuve et la procédure pénale prend le pas. Le mythe légalisé de la triangulation dramatique renforce cette vision. Il transforme la plainte en statut, et le statut en arme. Le conflit devient irréversible. Le rôle de médiation est disqualifié. L’ajustement devient impossible. Le symptôme domine la relation. Il est temps de proposer une alternative. L’ingénierie systémique relationnelle ouvre une autre voie. Elle propose une lecture active et structurée. Elle s’appuie sur les écarts ajustables, non sur les intentions figées.

Conclusion : dépasser les modèles hérités

Karpman, Maslow, Girard appartiennent à une culture de la fixation. Leurs modèles rassurent. Mais ils prolongent une tradition dualiste. Ils freinent la pensée dynamique. Une rupture devient nécessaire. Cette rupture de conception invite à rétablir une lecture co-régulatrice des tensions. Elle favorise la liberté d’action. Dépasser le triangle dramatique, c’est revisiter un paradigme pour créer une rupture épistémologique. C’est inscrire les interactions humaines dans une dynamique vivante, présente et structurée. C’est refuser les récits figés pour entrer dans une culture de l’ajustement. C’est repositionner la qualité relationnelle comme un levier d'une nouvelle culture collective. C’est rendre aux organisations leur capacité à intégrer les écarts comme leviers d’innovation relationnelle. Notre époque a de multiples aspects géniaux sur le plan technologique. Il est opportun de faire évoluer les mentalités. La posture ajustative devient un principe stratégique. L'ingénierie systémique relationnelle® en fournit l’ossature. Elle incarne une modernité consciente de ses interdépendances. Elle répond aux tensions du réel par la structure d’une pensée relationnelle. Elle transforme les postures fixes en dynamiques d’écoute et d’action. Elle convertit le soupçon en reconnaissance. Elle remplace la catégorisation par l’observation des rythmes, des potentiels et des intensités. Elle donne à la médiation une pleine portée de soutien à l'exercice renforcé de la liberté, en instrumentant la culture de l'apprentissage de la qualité relationnelle, autant avec soi qu'avec autrui. Il ne tient qu’à nous d’en faire un usage cohérent avec notre époque.
Par Management & Gouvernance
Lire la suite...
05Mai

Ajustativité dynamique et barycentrisme fractal : fondements formels de la Théorie de l’Ajustativité Générale (TAG)

Si vous connaissez les problèmes posés par Stanislaw Ulam, vous êtes bon pour être de mes lecteurs sur ce coup-là.

Cet article pose les fondations formelles de la Théorie de l’Ajustativité Générale (#TAG), une approche transdisciplinaire qui définit tout système dynamique comme une structure en ajustement permanent entre ses composantes, son contexte, et l’intensité de ses interactions. J'ai conçu la formule opérative ∆A = K ⋅ Φ ⋅ I, et déploie une modélisation géométrique fondée sur le DT-FRACTAL®, une structure fractale barycentrique à base de tétraèdres imbriqués centrés sur leur Fractocentre®. Ce cadre ouvre une voie d’unification entre la physique, la cognition, la biologie et l’ingénierie des systèmes complexes.

1. Introduction : limites des paradigmes prédictifs

Les modèles dominants en physique et en neurosciences reposent sur la prédictivité : anticiper le futur à partir de données passées. Or, dans les systèmes complexes, ouverts et sensibles à leur environnement, cette approche montre ses limites. La TAG propose un paradigme alternatif fondé sur l’ajustement dynamique présentiel.

2. La formule de l’ajustativité : ∆A = K ⋅ Φ ⋅ I

Cette formule constitue l’axiome opératif de la TAG :

  • ∆A : variation du niveau d’ajustativité d’un système

  • K : structure contextuelle (topologie, contraintes, cadre)

  • Φ : phase ou synchronisation dynamique entre les éléments

  • I : intensité des interactions effectives

Cette équation permet de modéliser le comportement d'un système vivant, physique ou cognitif sans recourir à une causalité linéaire.

3. Le modèle géométrique DT-FRACTAL®

J'introduisons ici la structure DT-FRACTAL® : un réseau fractal de tétraèdres organisés autour d’un barycentre dynamique appelé Fractocentre®. Chaque subdivision conserve une symétrie d’orientation et une isotropie relative par rapport au centre d’ajustement local.

4. Barycentrisme et cohérence : équation de stabilité

Une autre formule fondamentale de la TAG est donnée et représente le Fractocentre®, barycentre dynamique pondéré par le niveau d’ajustement local de chaque composant. Cette formule permet d’évaluer la stabilité d’un système quel que soit son degré de complexité.

5. Interprétations et domaines d’application

Ce formalisme permet d’aborder de façon unifiée :

  • La régulation dynamique des systèmes physiques non linéaires

  • Les processus d’ajustement en neurosciences (plasticité, attention, apprentissage)

  • Les équilibres biologiques adaptatifs

  • Les systèmes sociaux et organisationnels en tension

6. Conclusion et perspectives

La TAG et son formalisme fractal offrent un cadre robuste pour réinterpréter des phénomènes dispersés par discipline en une dynamique commune d’ajustement.

Avec ce modèle, j'ai apporté une solution à la question de la flottabilité isotrope (problème d’Ulam). Il en a résulté une déclinaison de simulations multiscalaires pour la validation du DT-FRACTAL® dans divers systèmes complexes, comme l'identification d'erreurs multiples. Et maintenant, je me retrouve dans la baignoire d'Archimède...

7. Ca vous branche : connectez-vous ! Je suis à votre écoute

Mots-clés : #ajustativité, #TAG, #systèmes complexes, #dynamique, #fractal, #cognition, #modélisation, #physique, #neurosciences, médiation, #management #sondage

Ps : toutes ces recherches et leurs applications font l'objet de protections internationales

Par Actualités Médiation, Articles, Management & Gouvernance, Neurosciences, Physique
Lire la suite...
03Mai

Ma raison, mon émotion, ma fantaisie

L'ouverture de mon site (2011) a pu correspondre à réaliser un portail de mes activités, centrées sur mes recherches dans divers domaines, parmi tout ce que déclenche la modélisation que j'ai conçue dans le courant des années 1977-1981. - avec Fernando Pessoa - esplanade du café " a brasileira", quartier du Chiado. En tout premier lieu, de cette modélisation qui est passée par une représentation géométrique, il en a résulté la médiation professionnelle. La rigueur scientifique de cette approche vient de l'exigence que j'ai apportée à ne jamais lâcher le référentiel. Maintenant, des formations en présentiel, distanciel et e-learning ont pris le relai. De nombreux sites sont là pour encadrer le sujet. Et des professionnels ont désormais intégré des compétences formidables, apportant des garanties de résultat à leurs intervention. L'école professionnelle de la médiation et de la négociation, la chambre professionnelle de la médiation et de la négociation, le réseau professionnel de la médiation et de la négociation - ViaMediation, la société de la médiation professionnelle, autant de structures qui portent ce projet orienté vers l'entente et l'entente sociale. Avec L'officiel de la médiation qui a succédé au Mediatoroscope, la médiation professionnelle, l'ingénierie systémique relationnelle, la qualité relationnelle ont leur fil d'actualité ouvert aux autres professionnels. Depuis, j'ai créé la théorie de l'ajustativité générale #TAG. Ma tribune est ouverte. Ce site personnel me permet une expression différente. Un livre posé sur la table du net. Des pages de partis pris. Mes positions, mes centres d'intérêt, mes humeurs, mes amusements... Ce sont les pages qui vont accumuler mes réflexions, combinant ma raison, mon émotion et ma fantaisie. Je vais y aborder ce par quoi je suis convaincu, ce qui me plait et ce qui me séduit, ou pas. Et parmi tout cela, le sérieux d'une recherche méthodologique, rationnelle, rigoureuse qui peut transformer les fondamentaux culturels à un point que je commence à pouvoir imaginer... juste en prenant un peu d'avance sur les générations futures, ce que je vous invite à faire.

Cet article a eu une première version à l'ouverture du site, le 4 mars 2011, à 14:50

Par Articles, galery rotative, Neurosciences, Physique
Lire la suite...