Physique

recherche en physique scientifique
02Août

A Bifractal Integer Sequence from Recursive Subdivision of the Stella Octangula

Croissance bifractale tétraédrique : une suite entière dérivée de la subdivision récursive de la Stella Octangula

Fractale stella octangula : une suite géométrique bifractale à potentiel théorique et industriel

Introduction philosophique

La manière dont nous voyons le monde conditionne profondément la manière dont nous le vivons. Cela peut sembler paradoxal, voire non académique, de commencer une étude mathématique par une réflexion d’ordre philosophique. Tant pis. Je n’ai pas été formé par les voies académiques traditionnelles : je suis autodidacte — en tout, y compris dans ce que j’appelle le tourisme existentiel. Certaines visions du monde projettent partout des arrondis, des courbes lissées, comme si adoucir les contours était la voie naturelle vers l’harmonie. C’est une illusion. Il n’y a rien de plus complexe, ni de plus exigeant, que d’arrondir véritablement les angles. Car ce geste — en apparence simple — exige un ajustement précis entre des éléments dissemblables, une gestion des tensions, et une tendance à négocier les points de rupture. On y retrouve les fondements des modèles de pensée économiques, administratifs, managériaux, avec tout le lexique qui les façonnent. C’est à partir de cette relecture fondatrice entre angle et arrondi, entre structure et adaptation, que je propose ici une approche bifractale : géométrique dans sa forme, mathématique dans son expression, philosophique dans sa visée.
Définie en 1509 par Luca Pacioli dans son traité De Divina Proportione, l’objet dont le nom de Stella Octangula sera donné par Johannes Kepler, est initialement pensée comme un symbole de proportion divine, dans l’esprit néoplatonicien de la Renaissance. Les illustrations de Léonard de Vinci lui confèrent un statut emblématique d’harmonie géométrique incarnée. Elle est redécouverte en 1609 par Johannes Kepler, qui y voit une forme parfaite, résultant de l’interpénétration de deux tétraèdres réguliers inversés. Plus tard, Leonhard Euler (1707–1783) formule la relation topologique fondamentale V−E+F=2, marquant une étape décisive dans la formalisation des structures closes. Ce progrès, en apparence neutre, tend paradoxalement à enfermer la Stella Octangula dans une lecture statique et figée. Ma proposition s’inscrit dans une tout autre logique : réouvrir la figure vers des perspectives dynamiques et systémiques, en la réinscrivant dans le champ des fractales, concept introduit dans les années 1970 par Benoît Mandelbrot. 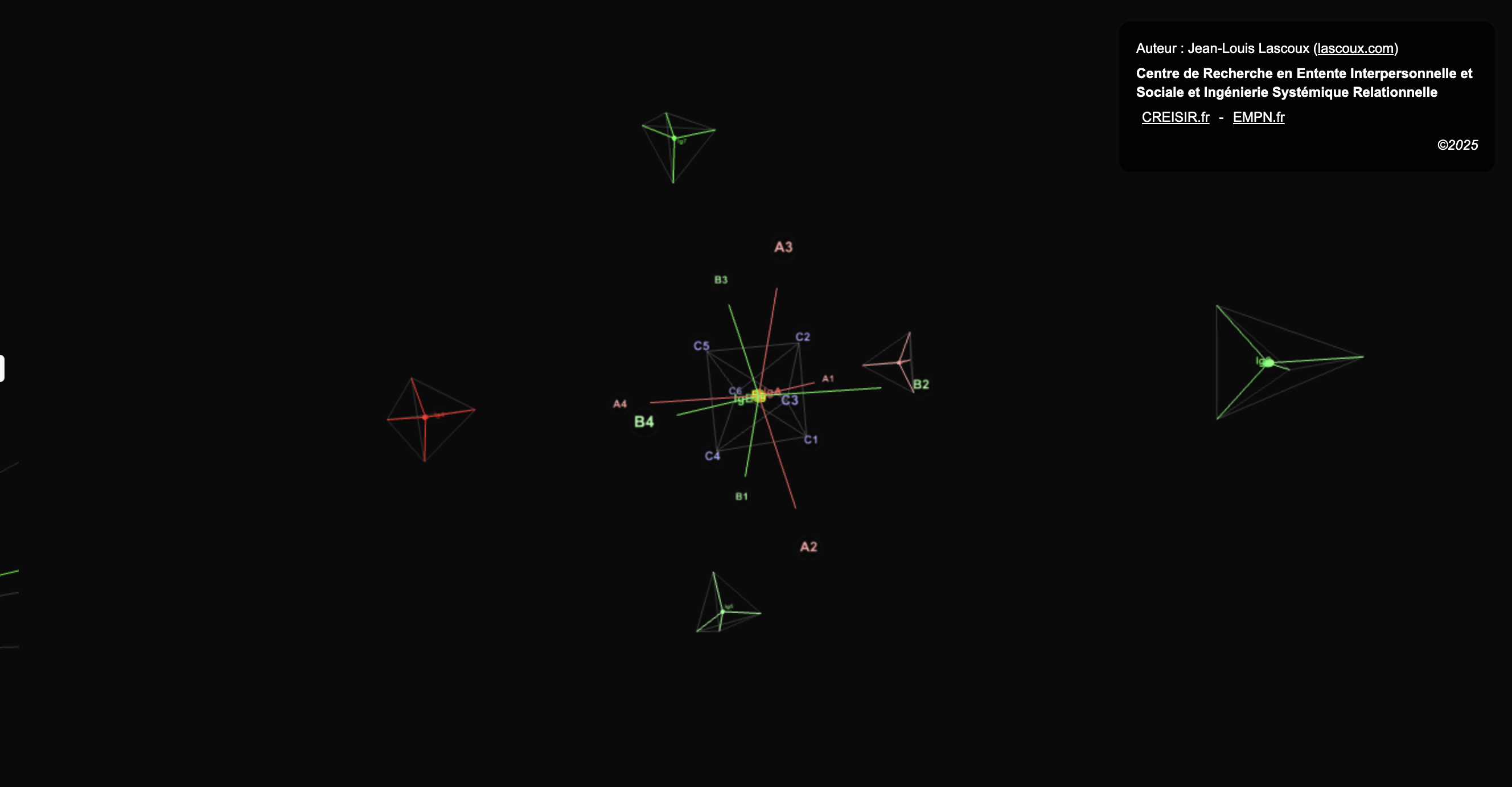L’application bifractale présentée ici vise à détacher la Stella Octangula de sa clôture topologique traditionnelle, pour en faire le support d’une croissance récursive ajustative, à la fois volumique (8-aire) et planaire (4-aire). 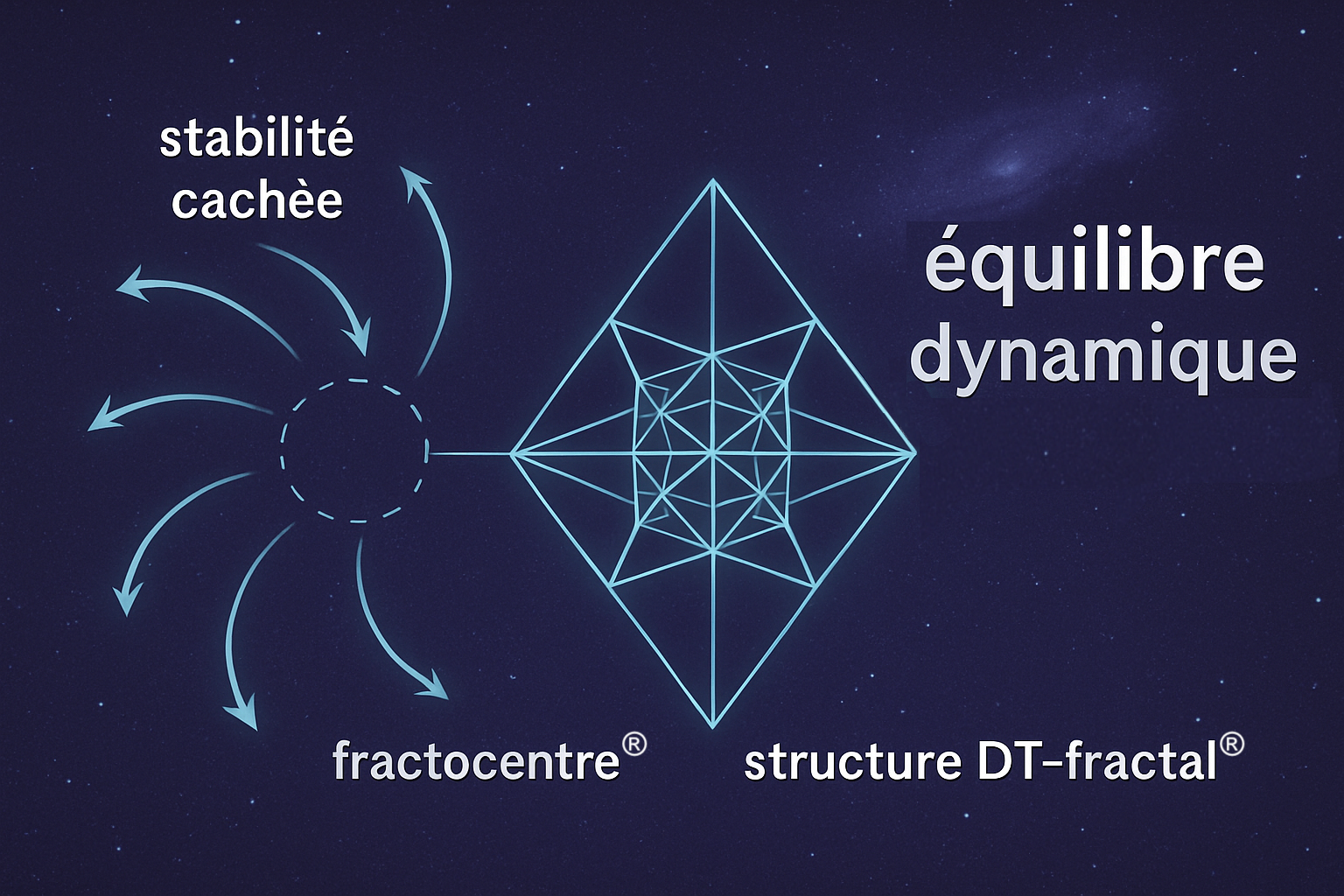C’est cette réinterprétation structurelle qui justifie mon choix de l’appeler désormais Bi-Tétraèdre Stellaire : ·       une appellation qui insiste sur son potentiel combinatoire, ·       sa dynamique de subdivision (organisée autour d’un Fractocentre®, et non d’un barycentre académique), ·       et sa capacité de déploiement hiérarchisé dans des modèles fractals d’ingénierie. Il ne s’agit plus d’un simple objet géométrique : c’est un modèle opératif, à la croisée de la précision mathématique, de la complexité fractale, et d’une visée systémique ajustative.
Dans cette recherche, la Stella Octangula– sur laquelle je reviens en nommant la structure « Bi-Tétraèdre stellaire », devient plus qu’un objet de curiosité géométrique : elle s’impose comme une autre forme de pensée. En effet, formée par l’interpénétration parfaite de deux tétraèdres opposés, elle incarne une tension équilibrée entre dualité et symétrie, entre stabilité et expansion. Ce n’est pas tant la figure elle-même qui importe, que la manière dont elle peut être subdivisée, régénérée, complexifiée — sans jamais perdre son principe d’organisation, avec une tonalité nouvelle associée à la liberté. Ce processus de subdivision, je le nomme ici bifractale, parce qu’il repose sur deux lois de croissance distinctes mais coordonnées. L’une est volumique, l’autre est planaire ; l’une s’appuie sur la démultiplication, l’autre sur la structuration. Ensemble, elles génèrent une dynamique hiérarchique d’une remarquable cohérence. Mais pourquoi s’y intéresser ? Parce qu’en modélisant cette croissance, en l’analysant sous forme d’une suite entière bien définie, nous accédons à plus qu’un simple jeu de nombres. Nous touchons à un modèle opératif d’ajustement. Un modèle qui relie le discret et le continu, le local et le global, l’ordre mathématique et la plasticité du réel. Ce lien entre pensée, structure et ajustement n’est pas nouveau. Il remonte à Pythagore, souvent considéré comme l’inventeur du mot philosophie – philo-sophia, l’amour de la sagesse. D’après Diogène Laërce[1], Pythagore aurait introduit ce terme pour désigner une posture de recherche désintéressée, tournée vers l’harmonie des lois universelles. Mais il ne s’agissait pas d’une sagesse vague ou contemplative : pour Pythagore, cette quête passait nécessairement par les nombres, les figures, les rapports. C’est à travers le langage mathématique et géométrique qu’il percevait l’ordre caché du cosmos, et c’est à travers cette exigence qu’il fondait une discipline intérieure. Revenir à la Stella Octangula, Bi-Tétraèdre Stellaire, avec une attention moderne, combinatoire, algorithmique, n’est donc pas un détournement du sens philosophique initial. C’est, au contraire, une fidélité profonde à l’idée pythagoricienne d’une sagesse en actes, qui cherche à comprendre le monde en le structurant — non pour le simplifier, mais pour mieux épouser sa complexité. C’est ainsi que j’ai développé un ensemble théorico-pratique qui touche à la fois au fonctionnement personnel (la théorie du cerveau corrélatif et de l’harmonisation ajustative (TCC-HA), la théorie de l’ajustativité temporelle (T.AJT), les deux réunies en Théorie de l’Ajustativité Générale (#TAG). C’est ambitieux, j’en conviens. Pour autant, cette approche est cohérente et se retrouve opérationnelle, en premier lieu, dans les contextes relationnels humains, puisque c’est là que j’ai développé la première application de mon modèle géométrique, la médiation professionnelle, la profession de médiateur fondée sur la qualité relationnelle et l’Ingénierie Systémique Relationnelle®. À partir de cette articulation entre structure géométrique, dynamique d’ajustement et modélisation relationnelle, nous pouvons formuler une expression mathématique rigoureuse de la croissance bifractale associée à la Stella Octangula. 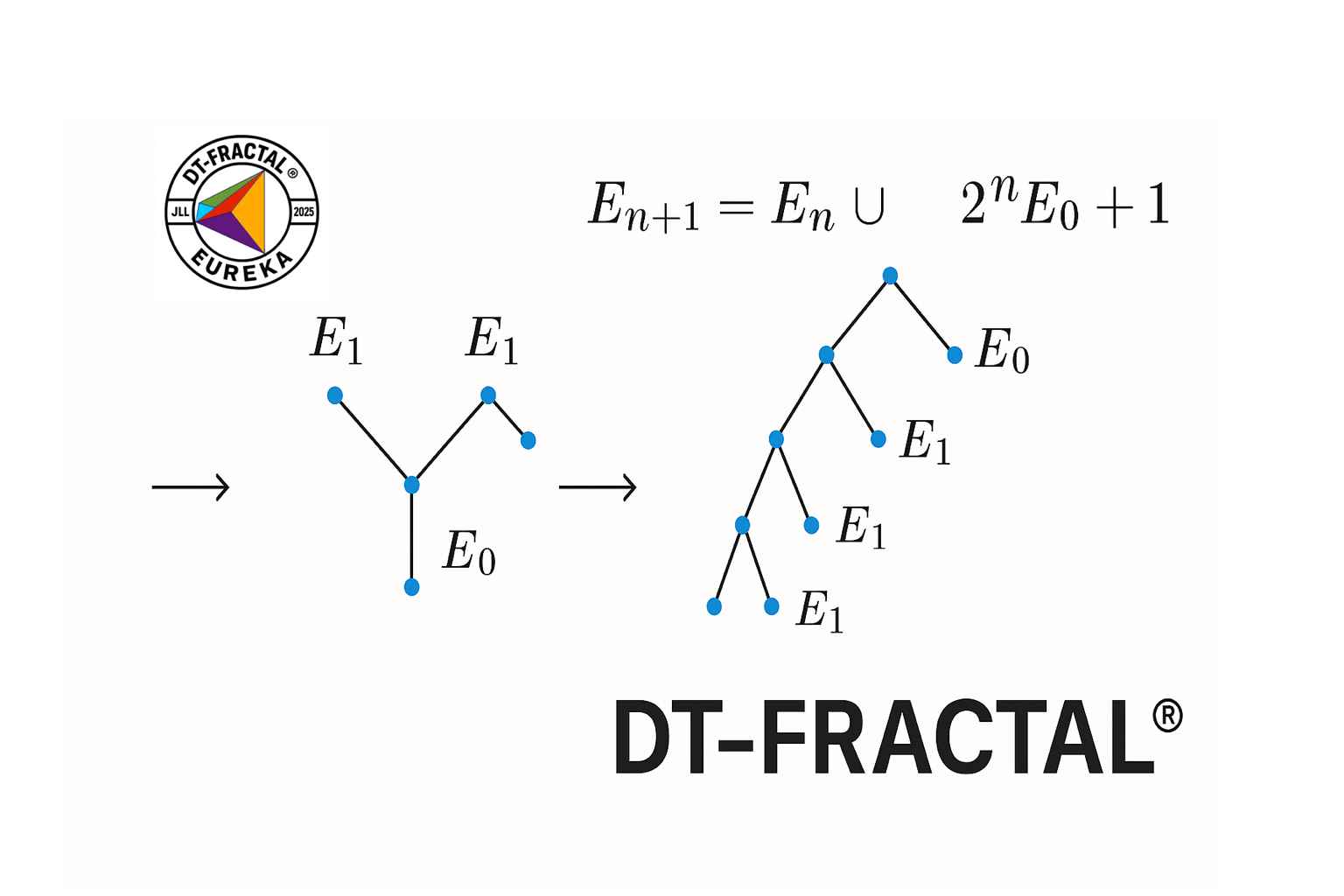Cette modélisation conduit naturellement à une suite entière a(n), dont chaque terme représente le nombre total de tétraèdres présents à l’itération n d’un processus récursif de subdivision. Ce processus repose sur deux lois complémentaires :
  • une subdivision volumique 8-aire, appliquée aux tétraèdres externes de la structure ;
  • une subdivision planaire 4-aire, centrée sur le cœur géométrique, le fractocentre®.
L’interaction de ces deux règles définit une dynamique de croissance hiérarchisée, que la suite a(n)a(n)a(n) encode intégralement.

Jean-Louis Lascoux – Bordeaux – 2025/08/02

[1] Diogène Laërce, Vies et doctrines des philosophes illustres, Livre VIII, §12. ____
Télécharger le document intégral avec en + les éléments mathématiques et géométriques (PDF) : A386761 : une suite géométrique issue de la subdivision tétraédrique d’un octaèdre régulier A386821 : Total tetrahedra in bifractal subdivision of stella octangula  
 
Par Actualités Médiation, Management & Gouvernance, Mathématiques & Géométrie, Physique
Lire la suite...
28Juil

Fractale de la stella octangula, un bi-tétraèdre stellaire : nouvelle séquence mathématique issue de la géométrie 3D

Introduction

En explorant les propriétés géométriques des tétraèdres réguliers, dont j'utilise les principes systémiques dans le cadre du développement de l'ingénierie systémique relationnelle, pour assurer l'harmonie conceptuelle, avec un équilibre méthodologique des raisonnements, j'ai développé un nouveau concept. Celui-ci met en regard deux tétraèdres réguliers susceptibles de se former en Stella Octangula - cette élégante étoile à huit branches formée par l'interpénétration de deux tétraèdres réguliers. Par delà la symbolique que peut représenter cette configuration que j'ai nommé Bi-Tétraèdre Stellaire, j'ai en fait découvert une structure fractale remarquable qui ouvre des perspectives sur les séquences mathématiques.

L'observation

La Stella Octangula est connue au moins depuis la Renaissance. Lorsqu'on la décompose par ce que l'on perçoit immédiatement, on identifie 8 tétraèdres externes et l'œuf central est un octaèdre. Ainsi, ce n'est qu'un début : cette décomposition n'est pas seulement géométrique - elle est le point de départ d'un processus fractal infini.

Un processus de subdivision volumique

À partir des 8 tétraèdres initiaux, on peut appliquer une subdivision récursive :

  1. Étape 1 : 8 tétraèdres (décomposition initiale)
  2. Étape 2 : Chaque tétraèdre se divise en 4 → 8 + 32 = 40 tétraèdres
  3. Étape 3 : Les 32 nouveaux se divisent → 40 + 128 = 168 tétraèdres
  4. Étape 4 : 168 + 512 = 680 tétraèdres

Une formule mathématique

Cette croissance suit une loi précise :

a(n) = 8 × (4ⁿ - 1) / 3

où n représente le nombre d'étapes de subdivision.

Une Séquence : OEIS

Les premiers termes de cette séquence sont :

8, 40, 168, 680, 2728, 10920, 43688, 174760, 699048, 2796200...

Des propriétés remarquables

  • Croissance exponentielle : facteur 4 à chaque étape
  • Structure fractale : auto-similarité à toutes les échelles
  • Symétrie octaédrique : héritée de la configuration initiale

Visualisation

Applications et Perspectives

Cette séquence trouve des applications potentielles en :

  • Géométrie computationnelle : maillages tétraédriques adaptatifs
  • Cristallographie : modélisation de structures complexes
  • Fractales 3D : nouvelle famille de fractales volumiques

Code de Génération

Pour les intéressés, voici comment générer les termes de cette séquence (Python) :

def stella_bitetrahedra(n): """Nombre total de tétraèdres après n subdivisions récursives 4-aires, en partant de 8 tétraèdres initiaux issus de la Stella Octangula.""" return 8 * (4**n - 1) // 3

# Afficher les 10 premiers termes for i in range(1, 11): print(f"a({i}) = {stella_bitetrahedra(i)}")

Et après ?

Cette découverte illustre comment des structures géométriques classiques peuvent encore révéler des propriétés mathématiques inédites. La stella octangula, étudiée depuis des siècles, a désormais un compagnon qui offre déjà une vaste richesse structurelle... Un ensemble de formules sont dans le tuyau pour enrichir ce travail qui ne va pas aller sans surprendre par ses perspectives...
Par Articles, Curiosité, Mathématiques & Géométrie, News, Physique
Lire la suite...
08Mai

Non, Poincaré, le monde ne tourne pas rond !

Bon, c'est vrai que c'est un peu facile, mais l'idée est là, dans l'humour du titre, très sérieusement. Hé oui, dans votre tête, la rondeur est rarement au rendez-vous, comme dans l'univers. Ca vous dit quelque chose cette expression : "Ca ne tourne pas rond dans sa tête !", qui sous-entend clairement que si ça tourne rond, alors, tout va bien.  Et si c'était une représentation infondée du monde ? De fait, la sphère peut paraître comme une forme parfaite. Pourtant, ce n'est pas très sûr. A y regarder d'un peu plus près, la sphère n'est pas aussi ronde que cela. Certes, elle paraît bien douce quand on la regarde dans une bulle. Elle nous entraîne dans le monde des mathématiques. A ce propos, vous connaissez la conjecture de Poincaré ? Il paraît que c'est l'un des grands mystères des mathématiques. Cette conjecture pose la question suivante : toute forme tridimensionnelle sans trou peut-elle être transformée en sphère ? Quelqu'un, en 2003, le mathématicien Grigori Perelman, a répondu oui. Pour cette affirmation, il s'est appuyé sur une méthode mathématique appelée "Ricci Flow" de Richard S. Hamilton.

Mais cette démonstration, bien qu’essentielle, ne dit rien sur la manière dont les formes réelles — celles que l’on observe dans la nature, dans les écosystèmes ou dans les structures sociales — s’organisent, se stabilisent ou s’ajustent.

C’est dans cette perspective que j'introduis un nouveau concept non mathématique au sens strict, mais opératif dans le cadre de la Théorie de l'Ajustativité Générale (TAG).

C’est là qu’intervient le concept de "fractosphéricité", un concept qui se conjugue avec la (TAG) que je développe en lien avec l'ingénierie systémique relationnelle®.

Définition du concept proposé

Fractosphéricité : propriété d’une forme tridimensionnelle simplement connexe (sans trou topologique), non sphérique, qui atteint néanmoins un état stable ou harmonieux dans un système complexe.

Autrement dit, une forme n’a pas besoin d’être sphérique pour être équilibrée. Certaines configurations fractales, polarisées, irrégulières — mais ajustées selon leur propre dynamique interne — peuvent manifester une stabilité comparable à celle d’une sphère.

Le modèle DT-FRACTAL®, issu de la TAG, explore précisément ces structures : des formes non sphériques, mais barycentriquement cohérentes, organisées par ajustement relationnel, et non par symétrie idéale.

Pourquoi cette approche est scientifique ?

Parce qu’elle ne rejette pas les théories antérieures (topologie classique, géométrie différentielle), mais les complète en proposant un nouvel angle de lecture pour les formes complexes observables.

La fractosphéricité introduit un cadre opératif d’analyse des formes ajustées dans les systèmes vivants, sociaux ou informationnels.

Ce que cela change

Cela ouvre une perspective nouvelle :

  • Un monde pas forcément centré, mais cohérent.
  • Un monde pas forcément symétrique, mais stabilisé par ajustement.
  • Une manière d’observer la réalité autrement, sans réduire l’harmonie à la perfection géométrique.
Donc : la fractosphéricité n'est pas une vérité mathématique à prouver comme un théorème, c'est une grille de lecture, un nouveau regard sur les formes de l'univers. Elle illustre comment la science peut avancer non pas en niant ce qui précède, mais en complétant les réponses par d'autres questions.
C'est ainsi que vous pouvez commencer à penser autrement.

Publication sur HAL.science :

Conjecture de Poincaré : au-delà de la sphère (Relecture ajustative)

 
Par Articles, Neurosciences, Physique
Lire la suite...
05Mai

Ajustativité dynamique et barycentrisme fractal : fondements formels de la Théorie de l’Ajustativité Générale (TAG)

Si vous connaissez les problèmes posés par Stanislaw Ulam, vous êtes bon pour être de mes lecteurs sur ce coup-là.

Cet article pose les fondations formelles de la Théorie de l’Ajustativité Générale (#TAG), une approche transdisciplinaire qui définit tout système dynamique comme une structure en ajustement permanent entre ses composantes, son contexte, et l’intensité de ses interactions. J'ai conçu la formule opérative ∆A = K ⋅ Φ ⋅ I, et déploie une modélisation géométrique fondée sur le DT-FRACTAL®, une structure fractale barycentrique à base de tétraèdres imbriqués centrés sur leur Fractocentre®. Ce cadre ouvre une voie d’unification entre la physique, la cognition, la biologie et l’ingénierie des systèmes complexes.

1. Introduction : limites des paradigmes prédictifs

Les modèles dominants en physique et en neurosciences reposent sur la prédictivité : anticiper le futur à partir de données passées. Or, dans les systèmes complexes, ouverts et sensibles à leur environnement, cette approche montre ses limites. La TAG propose un paradigme alternatif fondé sur l’ajustement dynamique présentiel.

2. La formule de l’ajustativité : ∆A = K ⋅ Φ ⋅ I

Cette formule constitue l’axiome opératif de la TAG :

  • ∆A : variation du niveau d’ajustativité d’un système

  • K : structure contextuelle (topologie, contraintes, cadre)

  • Φ : phase ou synchronisation dynamique entre les éléments

  • I : intensité des interactions effectives

Cette équation permet de modéliser le comportement d'un système vivant, physique ou cognitif sans recourir à une causalité linéaire.

3. Le modèle géométrique DT-FRACTAL®

J'introduisons ici la structure DT-FRACTAL® : un réseau fractal de tétraèdres organisés autour d’un barycentre dynamique appelé Fractocentre®. Chaque subdivision conserve une symétrie d’orientation et une isotropie relative par rapport au centre d’ajustement local.

4. Barycentrisme et cohérence : équation de stabilité

Une autre formule fondamentale de la TAG est donnée et représente le Fractocentre®, barycentre dynamique pondéré par le niveau d’ajustement local de chaque composant. Cette formule permet d’évaluer la stabilité d’un système quel que soit son degré de complexité.

5. Interprétations et domaines d’application

Ce formalisme permet d’aborder de façon unifiée :

  • La régulation dynamique des systèmes physiques non linéaires

  • Les processus d’ajustement en neurosciences (plasticité, attention, apprentissage)

  • Les équilibres biologiques adaptatifs

  • Les systèmes sociaux et organisationnels en tension

6. Conclusion et perspectives

La TAG et son formalisme fractal offrent un cadre robuste pour réinterpréter des phénomènes dispersés par discipline en une dynamique commune d’ajustement.

Avec ce modèle, j'ai apporté une solution à la question de la flottabilité isotrope (problème d’Ulam). Il en a résulté une déclinaison de simulations multiscalaires pour la validation du DT-FRACTAL® dans divers systèmes complexes, comme l'identification d'erreurs multiples. Et maintenant, je me retrouve dans la baignoire d'Archimède...

7. Ca vous branche : connectez-vous ! Je suis à votre écoute

Mots-clés : #ajustativité, #TAG, #systèmes complexes, #dynamique, #fractal, #cognition, #modélisation, #physique, #neurosciences, médiation, #management #sondage

Ps : toutes ces recherches et leurs applications font l'objet de protections internationales

Par Actualités Médiation, Articles, Management & Gouvernance, Neurosciences, Physique
Lire la suite...
03Mai

Ma raison, mon émotion, ma fantaisie

L'ouverture de mon site (2011) a pu correspondre à réaliser un portail de mes activités, centrées sur mes recherches dans divers domaines, parmi tout ce que déclenche la modélisation que j'ai conçue dans le courant des années 1977-1981. - avec Fernando Pessoa - esplanade du café " a brasileira", quartier du Chiado. En tout premier lieu, de cette modélisation qui est passée par une représentation géométrique, il en a résulté la médiation professionnelle. La rigueur scientifique de cette approche vient de l'exigence que j'ai apportée à ne jamais lâcher le référentiel. Maintenant, des formations en présentiel, distanciel et e-learning ont pris le relai. De nombreux sites sont là pour encadrer le sujet. Et des professionnels ont désormais intégré des compétences formidables, apportant des garanties de résultat à leurs intervention. L'école professionnelle de la médiation et de la négociation, la chambre professionnelle de la médiation et de la négociation, le réseau professionnel de la médiation et de la négociation - ViaMediation, la société de la médiation professionnelle, autant de structures qui portent ce projet orienté vers l'entente et l'entente sociale. Avec L'officiel de la médiation qui a succédé au Mediatoroscope, la médiation professionnelle, l'ingénierie systémique relationnelle, la qualité relationnelle ont leur fil d'actualité ouvert aux autres professionnels. Depuis, j'ai créé la théorie de l'ajustativité générale #TAG. Ma tribune est ouverte. Ce site personnel me permet une expression différente. Un livre posé sur la table du net. Des pages de partis pris. Mes positions, mes centres d'intérêt, mes humeurs, mes amusements... Ce sont les pages qui vont accumuler mes réflexions, combinant ma raison, mon émotion et ma fantaisie. Je vais y aborder ce par quoi je suis convaincu, ce qui me plait et ce qui me séduit, ou pas. Et parmi tout cela, le sérieux d'une recherche méthodologique, rationnelle, rigoureuse qui peut transformer les fondamentaux culturels à un point que je commence à pouvoir imaginer... juste en prenant un peu d'avance sur les générations futures, ce que je vous invite à faire.

Cet article a eu une première version à l'ouverture du site, le 4 mars 2011, à 14:50

Par Articles, galery rotative, Neurosciences, Physique
Lire la suite...
02Mai

Communiqué de presse : l’énigme du solide flottant de S. Ulam résolue par la #TAG

COMMUNIQUÉ DE PRESSE Une énigme mathématique vieille de 90 ans résolue grâce au modèle de l’ingénierie systémique relationnelle® qui a permis de développer la théorie de l'ajustativité générale #TAG. Certes, vous arrivez dans un environnement qui peut être très nouveau pour vous, celui de l'approche des effets relationnels et systémiques interactifs. N'excluez pas cette approche créatrice d'une rupture épistémologique : elle permet juste de prendre un peu d'avance sur les générations futures... 30 avril 2025 — Une percée scientifique majeure vient d’être réalisée dans le domaine des mathématiques appliquées et de la physique théorique. J'’annonce donc la résolution rigoureuse du célèbre problème d’Ulam n°19, formulé en 1935 dans le Scottish Book par mon approche relationnelle systémique. Ce problème posait la question suivante : “La sphère est-elle le seul solide homogène capable de flotter en équilibre dans toutes les orientations ?” Après près d’un siècle de spéculations et de tentatives partielles, une solution complète, démontrée analytiquement et validée numériquement, est désormais proposée grâce au modèle géométrique DT-FRACTAL®, développé dans le cadre de la Théorie de l’Ajustativité Générale (TAG). En 2022, le mathématicien Dmitry Ryabogin avait démontré qu’une sphère déformée pouvait également satisfaire les conditions du problème. Ici, nous franchissons un seuil conceptuel décisif : nous sortons non seulement du cadre des solides convexes, mais aussi du raisonnement binaire. Je propose une approche fondée sur la complexité relationnelle, par un raisonnement ternaire. La nouveauté est au rendez-vous, avec méthode, logique et rigueur comme principes fondamentaux. Une approche nouvelle et transdisciplinaire Sur le plan mathématique, le modèle repose sur une structure fractale isométriques, organisés autour d’un barycentre fixe, assurant une stabilité isotrope sans sphéricité. Trois théorèmes clés sont démontrés :
  • Nullité du moment résultant pour toute orientation ;
  • Validité volumique du modèle renforcé (version V4) ;
  • Unicité du Fractocentre®, centre dynamique d’ajustement.
Des simulations numériques couvrant ±45° d’orientation montrent une variation barycentrique inférieure à ΔG ≈ 10⁻¹⁷, confirmant la stabilité du système dans toutes les orientations. Une contribution à la science contemporaine Ce résultat dépasse les modèles classiques et ouvre un nouveau champ d’exploration fondé sur l’ajustement contextuel. Il offre des perspectives dans :
  • Hydrodynamique, robotique flottante, design biomimétique ;
  • Physique théorique : reformulation des lois d’interaction par ajustativité ;
  • Mathématiques appliquées : modélisation stable sans symétrie sphérique.
PRESS RELEASE A 90-year-old mathematical enigma solved thanks to the Relational Systemic Engineering® model, which led to the development of the Theory of General Adjustativity (#TAG). Admittedly, you are entering a domain that may be entirely new to you—that of interactive relational and systemic effects. Do not dismiss this approach, which initiates an epistemological breakthrough: it simply allows us to gain a small head start on future generations April 30, 2025 — A major scientific breakthrough has just been achieved in the field of applied mathematics and theoretical physics. I am Jean-Louis Lascoux, president of the Centre de Recherche en Entente Interpersonnelle et Sociale et Ingénierie Systémique Relationnelle (CREISIR), and I announce the rigorous resolution of the famous Ulam problem No. 19, formulated in 1935 in the Scottish Book. This problem posed the following question: “Is the sphere the only homogeneous solid capable of floating in equilibrium in all orientations?” After nearly a century of speculation and partial attempts, a complete solution—analytically demonstrated and numerically validated—is now proposed, thanks to the geometric model DT-FRACTAL®, developed within the framework of the Theory of General Adjustivity (TAG). In 2022, mathematician Dmitry Ryabogin demonstrated that a deformed sphere could also satisfy the conditions of the problem. Here, we cross a decisive conceptual threshold: we step beyond the framework of convex solids, and beyond binary reasoning. I propose an approach based on relational complexity, through a ternary reasoning process. Innovation is fully present, with method, logic, and rigor as foundational principles. A Novel and Transdisciplinary Approach From a mathematical standpoint, the model is based on an isometric fractal structure, organized around a fixed barycenter, ensuring isotropic stability without sphericity. Three key theorems are demonstrated:
  • Nullity of the resulting moment in all orientations;
  • Volumetric validity of the reinforced model (version V4);
  • Uniqueness of the Fractocentre®, a dynamic center of adjustment.
Numerical simulations covering ±45° of orientation show a barycentric variation of less than ΔG ≈ 10⁻¹⁷, confirming the system’s stability in all orientations. A Contribution to Contemporary Science This result surpasses classical models and opens a new field of exploration based on contextual adjustment. It offers new perspectives in:
  • Hydrodynamics, floating robotics, and biomimetic design;
  • Theoretical physics: reformulating the laws of interaction through adjustivity;
  • Applied mathematics: stable modeling without spherical symmetry.
Par Articles, Physique
Lire la suite...
01Mai

Du stock d’énergie à l’ajustement dynamique : repenser l’Univers

Depuis que la science a ouvert les pages blanches du grand livre universel, les scientifiques cherchent à en écrire les chapitres. Les hypothèses se succèdent. Les paradoxes des récits anciens sont remplacés par des énigmes qui paraissent fondamentales.

  • Pourquoi l’Univers semble-t-il « manquer » de matière visible ?
  • Pourquoi les théories de l’infiniment grand (relativité) et de l’infiniment petit (quantique) résistent-elles à leur unification ?
  • Pourquoi certaines observations laissent-elles penser que l’Univers serait en expansion, voire que cette expansion s’accélérerait – sans qu’il soit exclu que cette impression soit liée à des effets inertiels ou perceptifs, analogues à l’illusion d’ascension que donne un ralentissement brusque, comme celui d’un parachutiste dont le parachute s'ouvre ?

Ainsi, avec l'identification de ses propres énigmes, la science progresse. Aujourd’hui, si des réponses (souvent provisoires) sont proposées : matière noire, énergie noire, les modèles quantiques restent encore inachevés. Pour autant, aucune réponse ne parvient à formuler véritablement des idées satisfaisantes pour notre compréhension du réel.

Il semble néanmoins possible d'écrire un nouveau chapitre grâce à une approche novatrice qui me fait énoncer quelques impertinences. Certes, j'y suis entraîné : déjà, j'ai commis ce genre d'infraction dans le champ de la médiation des relations conflictuelles et le chemin n'est pas encore débrousaillé. Maintenant, je propose ma structure DT-FRACTAL® et le Fractocentre® ajustatif, issus de la Théorie de l’Ajustativité Générale (TAG) que je me plais à enrichir de jour en jour, pour aborder la science de la physique, de la géométrie, de la mécanique, de la biologie, etc...

Cette proposition n’est pas une simple intuition, elle repose sur des modélisations des calculs analytiques et une correspondance cohérente avec des phénomènes observés.

Un changement de perspective : de la force brute à la finesse de l'ajustement

Au lieu de supposer que toute structure est dominée par des stocks de masse ou d’énergie fixes, mon idée est de proposer une vision dynamique :

Ce qui compte n’est pas la quantité brute, mais la qualité relationnelle entre les composantes d’un système, une qualité que j'énonce avec le terme d'ajustement.

Cet ajustement peut être formalisé par une relation simple :

où :

  • A représente le niveau d’ajustativité d'un système,
  • K le contexte dans lequel il évolue,
  • Φ la phase ou la synchronisation active entre ses éléments,
  • I l'intensité réelle des interactions.

Ainsi, plutôt que de mesurer des stocks statiques, nous mesurons la qualité dynamique de cohérence dans l’interaction.

Cette nouvelle approche peut permettre de comprendre que :

  • Le "manque" de matière visible n’est vraisemblablement pas un vide qui serait à combler par une évolution expansive, mais une compensation naturelle entre structures fractales d’ajustement.

  • L’expansion accélérée de l’Univers n’est pas une force extérieure inexplicable, mais le résultat d’un rééquilibrage dynamique au sein d'un réseau global de corrélations.

  • La gravitation et la mécanique quantique ne s’opposent pas : elles décrivent des niveaux différents d’ajustativité fractale dans la matière et les structures relationnelles de l’espace.

  • Le temps, quant à lui, ne peut pas être considéré comme une dimension équivalente aux dimensions spatiales, il correspond plutôt une dynamique locale d’ajustement, résultant de la synchronisation corrélative des systèmes en interaction. Ainsi, il n'est pas un contenant universel, mais une émergence locale de la qualité d’ajustement.

Le fractocentre : la clé de l’équilibre caché

Au cœur de cette révolution conceptuelle se trouve le Fractocentre® : un point dynamique, un repère barycentrique mobile des ajustements internes d’un système.

Quelle que soit la complexité de la structure, tant que le Fractocentre® reste contenu et stabilisé par les flux internes, le système reste cohérent, stable, adaptatif.
S'il dérive au-delà d’un seuil critique, alors apparaissent instabilités, émergences ou effondrements (ex : instabilités de galaxies) ; il en va ainsi dans le champ des relations humaines, de soi aux autres, de l'état satisfaisant à la destructuration.

Ainsi, dans l’Univers dont la nature vivante (systémique !) n'a pas la même signification que celle de l'existence biologique, mais qui repose sur les mêmes lois organiques, la stabilité observée à grande échelle ne serait pas due à une masse invisible ou à une force mystérieuse :

Elle serait la manifestation naturelle de l'ajustement dynamique entre les structures existantes, suivant un modèle fractal, continu et adaptatif.

Ce que cette résolution change concrètement

Après m'être consacrée aux aspects systémiques relationnels de la vie humaine, j'élargis ma contribution, ou plutôt je réajuste ma contribution, puisqu'en réalité ma pensée s'est structurée à partir d'une modélisation que j'ai patiemment appliquée aux phénomènes relationnels. Maintenant, l'œuvre est délicate, mais ceux qui s'y pencheront pourront en extraire une instrumentation au service d'un réajustement global de nos organisations sociétales.

  • En physique fondamentale : repenser les lois de la gravitation et de la cosmologie à partir d’une dynamique ajustative et non d’une simple mécanique inertielle.

  • En ingénierie : concevoir des matériaux, des réseaux et des systèmes énergétiques capables de s’auto-ajuster sans rupture.

  • En biologie : comprendre les organismes vivants comme des systèmes d’ajustement fractal et non comme de simples machines thermodynamiques.

  • En cognition et en sociologie : modéliser la conscience, l’apprentissage et l’organisation sociale comme des processus de synchronisation ajustative, multi-niveaux.

Vers un nouvel âge scientifique

Ce passage du paradigme de la "force" au paradigme de "l'ajustement" ouvre une ère nouvelle :

Non plus prédire un état final, mais comprendre comment l’équilibre évolue sans se perdre.

Dans l’esprit même de la transition ouverte lorsque des penseurs ont fait quitter à la l'idée d'un espace neutre pour celle d'un espace actif —, je propose avec la #TAG une lecture où le principe relationnel systémique, soit l'interaction elle-même, devient le véritable substrat du réel.

Loin d'une rupture violente avec la science classique, c’est une prolongation naturelle, un affinement de notre regard sur le réel, dans cette marche universelle qui fait de nous des touristes exigeants et souvent inutilement prédateurs. Un regard qui voit désormais non seulement les masses et les énergies, mais aussi - métaphoriquement - les respirations silencieuses qui maintiennent l'équation de l'équilibre et de l'harmonie universelle.

À ceux qui cherchent à comprendre non seulement ce qui est, mais comment ce qui est persiste, la #TAG ouvre une voie opérative, sensible, rigoureuse.

Par Articles, Physique
Lire la suite...
24Avr

La lumière qui s’adapte sans puce ni logiciel

Et si une ampoule pouvait s’allumer sans électronique, sans puce, sans application mobile… et pourtant s’ajuster en temps réel à son environnement ?

C’est le pari de cette technologie émergente qui repose non pas sur la programmation, mais sur les propriétés physiques des matériaux eux-mêmes.

Ni intelligence artificielle, ni connectivité. cette ampoule sans circuit adapte sa lumière selon la tension, la température, ou l’humidité ambiante. Pas grâce à un microprocesseur, mais par la combinaison passive de matériaux à mémoire de forme, à transition de phase, et d’un agencement fractal. Son cœur – le Fractocentre® – régule l’ensemble comme le ferait un organisme, sans avoir besoin de le commander.

Derrière cet objet se cache une logique bien plus large : celle de la Théorie de l’Ajustativité Générale (TAG). Issue de mes recherches en neurosciences, communication et Ingénierie systémique relationnelle®, cette théorie propose une nouvelle manière de concevoir les systèmes complexes : non plus en les pilotant de l’extérieur, mais en favorisant leur capacité à s’ajuster dynamiquement selon les interactions en cours.

Dans cette optique, j'ai adressé une proposition de collaboration R&D au CEA et au CNRS de Grenoble, dans le cadre du programme France 2030 – LUMA, pour explorer le potentiel industriel et scientifique de l'ampoule DT-Fractal. Cette initiative vise à démontrer que les principes de l'ajustativité peuvent apporter des alternatives technologiques sobres, robustes et reproductibles.

Je reste également ouvert à toute proposition de partenariat, institutionnel ou industriel, pour développer d’autres déclinaisons applicatives de la formule ajustative ΔA, dans les domaines de l’énergie, de la santé, de l’architecture ou des interfaces bio-inspirées.

Par Articles, Physique
Lire la suite...
20Avr

L’eau n’a plus le temps : accélérons ses particules

Vers une fluidique ajustative : modélisation corrélative de la viscosité effective en milieu nanoconfiné

Résumé

Je propose une nouvelle approche conceptuelle et opérationnelle de la viscosité effective dans les systèmes fluidiques nanoconfinés, fondée sur mes théories de l'ajustativité (TCC-HA / T.AJT ⇒ TAG).

Une formule innovante, issue de mes travaux, introduit un facteur d'ajustement corrélatif représentant le degré d'harmonie dynamique entre le fluide et les parois confinantes. Cette approche permet d'intégrer les phénomènes de superlubrification, de glissement quantique et de transport optimisé dans un cadre unifié d'interaction adaptative, ouvrant la voie à une génération de dispositifs fluidiques auto-ajustables.

Cette approche, ainsi que la formule sous-jacente, font l’objet de travaux en cours et sont protégées par leur antériorité de conception.

Introduction

La recherche transversale d'interlocuteurs pour mettre en pratique les fondamentaux de la théorie du cerveau corrélatif et de l'harmonisation ajustative (TCC-HA) et de la théorie de l'ajustativité générale (#TAG) m'a conduit à découvrir les travaux de Lyderic Bocquet et Radha Boyang.

Mon objectif ici est de démontrer une nouvelle fois la transversalité de mes concepts et développements. Cette fois, je vais plus loin dans la démonstration, car ce sujet m'apparaît formidable, compte tenu qu'il s'agit de travailler sur l'un des éléments fondamentaux de la vie humaine : l'eau. Les conséquences d'une augmentation de l'écoulement de l'eau, c'est-à-dire de sa fluidification, peuvent apporter une révolution énergétique, non seulement pour sa circulation mais aussi pour sa captation et son utilisation dans divers domaines industriels et environnementaux.

Pour réaliser ce travail, il me suffit d'avoir mon modèle de base, les composantes de mes travaux en Ingénierie Systémique Relationnelle® (tout n'est-il pas relation ?), ma dubitativité fondamentale et une bonne salve de réflexivité accompagnée par les connaissances accessibles aux IA.

L'eau de là...

Et si on changeait de paradigme ? De la prédictivité, on passe à l'ajustativité, de l'idée du futur, on passe à l'immédiateté, de l'intentionnalité supposée on passe à l'observation effective 360°, des croyances et des incertitudes on passe à carpe diem...

La nanofluidique est un domaine en pleine expansion, mais les comportements inattendus des fluides à très petite échelle restent difficiles à comprendre. Débits ultra-rapides, glissement aux parois, conductivités ioniques anormales, effets neuromorphiques : ces phénomènes peuvent être perçus comme des anomalies par rapport au cadre classique de la mécanique des fluides.

Je propose une relecture de ces effets à partir d'une hypothèse centrale :

Le comportement du fluide dans un environnement nanoconfiné n'est pas déterminé uniquement par des lois structurelles, mais émerge d'un processus d'ajustement dynamique entre les entités en interaction.

Ce principe s'inscrit dans le cadre théorique de la TAG, selon laquelle un système tend à réduire ses écarts internes (bruit, déphasage, dissipation) par ajustement corrélatif avec son environnement.

Aller, c'est parti pour rendre l'eau encore plus fluide

L'ambition de cet exposé est d’accompagner les recherches engagées avec l’idée de rendre l'eau « énergétiquement 1 000 fois plus fluide » : non pas en modifiant sa composition, mais en créant les conditions d'un écoulement où la dissipation d'énergie est minimisée grâce à un ajustement optimal entre fluide et structure.

Cela signifie :

  • Moins de pression nécessaire
  • Moins de bruit et d’instabilité
  • Des systèmes fluidiques à intelligence passive embarquée

Formulation

La viscosité effective ne serait plus une donnée figée, mais le reflet d’une interaction réussie entre fluide et structure. Elle est modélisée comme une viscosité de référence modulée par une fonction d’ajustement dynamique : plus la synchronisation est grande, plus la fluidité augmente.

Par exemple : dans un canal aux parois vibrantes, l’ajustement pourrait être mesuré par la réduction de la musicalité générée par le fluide en mouvement.

Mise en œuvre expérimentale

  1. Canaux rigides vs adaptatifs → Comparer en fonction du type de paroi
  2. Spectre de bruit → Identifier signatures vibratoires et acoustiques de l’ajustement
  3. Fréquence vibratoire contrôlée → Tester l’effet de l’accord entre fluide et structure
  4. Corrélation entre ajustement et dissipation → Évaluer la réduction énergétique comme signature de l’harmonie

Perspectives concrètes

Cette modélisation ouvre des pistes concrètes dans deux domaines vitaux :

💧 Séparation eau-sel : → Une membrane auto-ajustable peut désaliniser l’eau avec une moindre dépense énergétique

⚡ Production d’énergie osmotique : → Un système accordé en temps réel maximise le rendement du gradient salin

Ces deux usages confèrent à cette approche un potentiel industriel et écologique majeur, en lien avec les travaux sur les membranes à nanotubes, les dispositifs d’énergie bleue et les technologies fluidiques adaptatives.

Pour conclure

Dois-je appeler à une exploration transdisciplinaire de cette piste, alliant physique, cognition et ingénierie adaptative ? Je laisse la question ouverte — et je suis prêt à en discuter avec ceux qui soutiennent les projets innovants?

#Tags

#TCCHA #TAG #fluidique #nanofluidique #ajustativité #énergiebleue #eau #technologie #innovation #physique #neurosciences #R&D #systèmescomplexes #désalinisation #mécanique #énergétique

#Physicien·ne #Ingénieur·e #mécanique / #énergétique / #systèmes #sciences #Roboticien·ne / #mécatronicien·ne #Neuroscientifique #computation #Bio-ingénieur·e / #biomécanicien·ne #thermique #HVAC #gouvernance #organisation #innovation / #R&D

Par Articles, Physique
Lire la suite...
12Avr

La matière en résonance avec la #TAG : quand les matériaux peuvent interagir à la demande

Imaginez un peu : les matériaux du futur ne réagiront plus seulement à des forces, mais s’ajusteront activement à leur environnement ? Inspirée des théories du cerveau corrélatif et de l’harmonisation ajustative - TCC-HA  et de l’ajustativité temporelle-T.AJT, la formule ΔA = K ⋅ ϕ(t) ⋅ I(t) propose une nouvelle lecture des comportements matériels, fondée sur la résonance, la structure et l’intensité. Cette physique de l’ajustement pourrait bien transformer nos technologies, nos interactions, et notre manière de penser la matière. Ce changement de paradigme s’enracine dans des recherches sur les mécanismes de dégradation relationnelle et les dynamiques de qualité relationnelle.

Depuis la formulation d'Albert Einstein en 1905 de la fameuse équation liant masse et énergie, nous savons avec E=MC2 que la matière contient un potentiel colossal, même dans ses formes les plus discrètes. Cette révolution a conduit aux grandes avancées de la physique du XXᵉ siècle : fission, fusion, propulsion, et détection de particules. Mais aujourd'hui, alors que la science explore la frontière du vivant, des systèmes intelligents, et de la matière programmable, une nouvelle question émerge :

Et si l'énergie ne résultait plus seulement d'une conversion de matière, mais d'une transformation continue liée à l'environnement même du matériau ?

Le Monde est fait de relations et de corrélations

C’est dans cette perspective que s’inscrit une nouvelle approche inspirée des travaux en ingénierie systémique relationnelle, et plus spécifiquement de la Théorie de l’Ajustativité Générale (#TAG). Cette théorie propose de dépasser les modèles fondés sur la prédiction linéaire, pour introduire une dynamique d’ajustement permanent et contextuel. Elle s’inscrit résolument dans une démarche éthique, consciente des risques qu’a fait peser l’instrumentalisation historique de la formule d’Einstein.

Car en effet, si la formule a démontré que toute masse contenait une énergie potentielle phénoménale, son application a aussi donné naissance à des usages destructeurs. À l’inverse, la TAG propose de penser l’énergie non plus comme une quantité brute à exploiter, mais comme une variation d’état ajustée à l’environnement. Cette lecture transforme radicalement notre rapport à la matière, au vivant, et au temps.

Dans cette optique, une nouvelle loi émerge, dont la formulation mathématique commence à se stabiliser. Elle s'exprime ainsi :

ΔA = K⋅ ϕ ⋅I

Cette formule agit comme un modèle de comportement, et ce sont les simulations qui vont :

  • lui donner une forme observable (courbes, oscillations, seuils, transitions),
  • tester différents contextes : biologique, thermique, énergétique, interactionnel,
  • valider des interprétations (ex. : phase critique, résonance, saturation…),
  • et ouvrir vers des équations différentielles, fractales ou quantiques, selon l’approche.

Une dynamique, trois dimensions fondamentales

On considère ainsi que la variation d’un état matériel — qu’il s’agisse de sa forme, de sa tension interne ou de sa fonction — peut résulter de l’interaction entre trois dimensions :

  • La structure propre du matériau, qui définit sa capacité à se transformer.
  • Le rythme ou la phase de son activation, autrement dit sa manière de vibrer, de pulser, d’être synchronisé à une fréquence donnée.
  • Et enfin, l’intensité de l’interaction reçue, que ce soit un champ électrique, une force mécanique, une onde ou une chaleur localisée.

Ce modèle ne décrit pas une causalité brute. Il vise à rendre compte d’un phénomène plus subtil : l’ajustement dynamique d’un système à ce qui le traverse.

Matériaux d'ajustement : domaines d'application

  1. Militaire : blindages morphologiques réactifs, drones à structure variable, camouflage adaptatif. Rythme d'onde détectée Intensité électromagnétique ou acoustique locale
  2. Chirurgical : stents à déploiement ajusté, implants bio-résonants, tissus intelligents. Phase biologique (pulsation, flux nerveux) Pression, température, signal d'activation
  3. Bioinspiration et textile : vêtements adaptatifs, matériaux thermo-réactifs, micro-robots mous. Cycles environnementaux (chaleur, humidité) Stimuli biochimiques ou électrostatiques
  4. Architecture vivante : structures qui s'ouvrent, respirent ou se contractent en fonction des cycles environnementaux. Répétitions solaires, variations climatiques Pression, lumière, vibration externe

Simulation : un comportement fractal-oscillatoire

En modélisant les rythmes d’activation comme des oscillations lentes, et les stimulations comme des impulsions modulées, on obtient des comportements dynamiques qui rappellent ceux des systèmes vivants. Les matériaux se mettent à vibrer, pulser, et s’ajuster, non plus comme des objets passifs, mais comme des agents corrélatifs. Ce comportement, déjà observé dans certains polymères et alliages à mémoire de forme, ouvre la voie à une ingénierie plus fine, plus vivante.

 

Illustration de la variation ajustative ΔA(t) d’un polymère électroactif soumis à une stimulation électrique de 100 V à 1 kHz.

Ce type de matériaux qui répondent comme dans ta simulation existent, mais ne sont pas encore interprétés ni conçus selon une physique de l’ajustement intégrée, et c’est là que cette formule ΔA = K·ϕ·I prend tout son sens : elle peut aussi devenir le langage transversal de la matière intelligente.

Vers une physique de l’Ajustativité

Ce que cette nouvelle approche esquisse, c’est une transition : de la physique de l’énergie brute à une physique de l’ajustement. Elle ne cherche pas à rejeter les fondements classiques, mais à les enrichir d’une perspective plus dynamique, plus contextuelle. Elle postule que la matière peut être sensible, au sens où elle serait capable de se régler elle-même — comme un instrument accordé à l’univers.

En bref

Ressources

· Einstein, A..

o Zur Elektrodynamik bewegter Körper. Annalen der Physik, 322(10), 891–921. (1905)

o Comment je vois le monde (1934)

· Lascoux, J.-L.

o   Théorie de l’Ajustativité Générale #TAG. (en cours)

o   Dictionnaire encyclopédique de la médiation. ESF Sciences Humaines. (2018)

o   Livre blanc sur l'intelligence artificielle, la pensée et la conscience. Médiateurs Éditeurs. (2024)

o Et tu deviendras médiateur (2007)

o   Etude Systémique des Interactions en Communication -SIC www.etudesic.com

·       EPMN (École Professionnelle de la Médiation et de la Négociation) : www.epmn.fr

·       CREISIR (Centre de Recherche en Entente Interpersonnelle et Systémique Relationnelle) : www.creisir.fr

     
Par Articles, Physique
Lire la suite...